こんにちは。東久留米市の学習塾塾長です。
今回は、2012年筑波大附属駒場高入試に出題された整数問題を取り上げます。
問題は、
「次の問いに答えよ。
(1) 1×2×3×・・・×2012 のように、1から2012までの整数をすべてかけてできた数は、一の位から0がいくつか連続して並んでいる。0は一の位から何個連続して並んでいるか。
(2) 2013から4024までの整数をすべてかけてできた数は、一の位から0がいくつか連続して並んでいる。0は一の位から何個連続して並んでいるか。
(3) 1からaまでの整数をすべてかけてできた数は、一の位から0がちょうど2012個連続して並んだ。aの値として考えられるものをすべて答えよ。なお、aは1より大きい正の整数とすろ。」
です。
n! に含まれる素因数pの個数Nは、
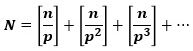
ここで、[x]はxを超えない最大の整数
と表せることを利用すれば簡単です。
それでは(1)から始めましょう。
一の位から連続して並ぶ0の個数は、10で割り切れる回数、つまり、2で割り切れる回数と5で割り切れる回数の少ないほうになります。
1×2×3×・・・×2012 の2で割り切れる回数は、
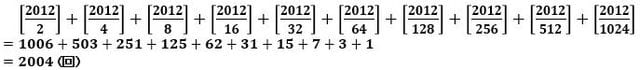
です。
一方、5で割り切れる回数は、

です。
したがって、一の位から連続して並ぶ0の個数は 501個 で、これが答えです。
次に(2)です。
5で割り切れる回数は2で割り切れる回数より少ないので、5で割り切れる回数だけを勘定します。
1×2×3×・・・×4024 の5で割り切れる回数は、
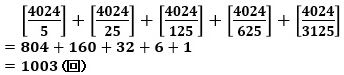
です。
(1)から、1×2×3×・・・×2012 の5で割り切れる回数は501回なので、2013×2014×2015×・・・×4024 の5で割り切れる回数は、
1003-501=502(回)
になります。
したがって、一の位から連続して並ぶ0の個数は 502個 で、これが答えです。
最後の(3)です。

の5で割り切れる回数は、

です。
つまり、
k=5のとき、781(回)
k=6のとき、3906(回)
で、aのおよその値は、
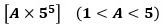
と表すことができます。
ここで、

の5で割り切れる回数を見積もると、
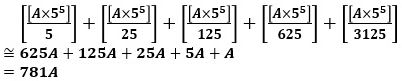
から、これが2012になるのは、
A=2012/781
のときで、このときaのおよその値は、
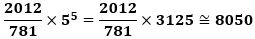
になります。
ここで、1×2×3×・・・×8050 の5で割り切れる回数を計算すると、
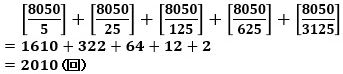
で、まだ2回足りません。
そこで、5×2=10を足して8060として、1×2×3×・・・×8060 の5で割り切れる回数を計算すると、
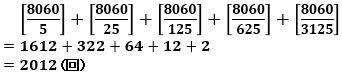
になりました。(1×2×3×・・・×8059 の5で割り切れる回数は2012回より少なくなります)
さらに、8061、8062、8063、8064 は5を約数にもたないので、1からこれらの数までの整数をすべてかけてできた数の5で割り切れる回数は2012回になります。
以上から、aの値として考えられるものは 8060、8061、8062、8063、8064 で、これが答えです。
簡単な問題です。
今回は、2012年筑波大附属駒場高入試に出題された整数問題を取り上げます。
問題は、
「次の問いに答えよ。
(1) 1×2×3×・・・×2012 のように、1から2012までの整数をすべてかけてできた数は、一の位から0がいくつか連続して並んでいる。0は一の位から何個連続して並んでいるか。
(2) 2013から4024までの整数をすべてかけてできた数は、一の位から0がいくつか連続して並んでいる。0は一の位から何個連続して並んでいるか。
(3) 1からaまでの整数をすべてかけてできた数は、一の位から0がちょうど2012個連続して並んだ。aの値として考えられるものをすべて答えよ。なお、aは1より大きい正の整数とすろ。」
です。
n! に含まれる素因数pの個数Nは、
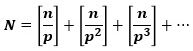
ここで、[x]はxを超えない最大の整数
と表せることを利用すれば簡単です。
それでは(1)から始めましょう。
一の位から連続して並ぶ0の個数は、10で割り切れる回数、つまり、2で割り切れる回数と5で割り切れる回数の少ないほうになります。
1×2×3×・・・×2012 の2で割り切れる回数は、
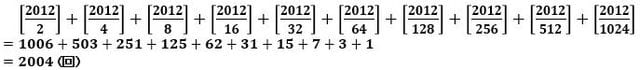
です。
一方、5で割り切れる回数は、

です。
したがって、一の位から連続して並ぶ0の個数は 501個 で、これが答えです。
次に(2)です。
5で割り切れる回数は2で割り切れる回数より少ないので、5で割り切れる回数だけを勘定します。
1×2×3×・・・×4024 の5で割り切れる回数は、
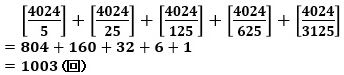
です。
(1)から、1×2×3×・・・×2012 の5で割り切れる回数は501回なので、2013×2014×2015×・・・×4024 の5で割り切れる回数は、
1003-501=502(回)
になります。
したがって、一の位から連続して並ぶ0の個数は 502個 で、これが答えです。
最後の(3)です。

の5で割り切れる回数は、

です。
つまり、
k=5のとき、781(回)
k=6のとき、3906(回)
で、aのおよその値は、
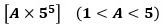
と表すことができます。
ここで、

の5で割り切れる回数を見積もると、
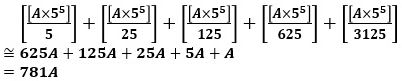
から、これが2012になるのは、
A=2012/781
のときで、このときaのおよその値は、
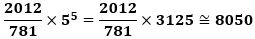
になります。
ここで、1×2×3×・・・×8050 の5で割り切れる回数を計算すると、
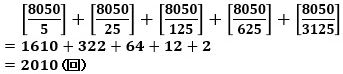
で、まだ2回足りません。
そこで、5×2=10を足して8060として、1×2×3×・・・×8060 の5で割り切れる回数を計算すると、
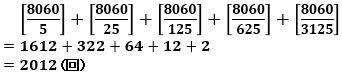
になりました。(1×2×3×・・・×8059 の5で割り切れる回数は2012回より少なくなります)
さらに、8061、8062、8063、8064 は5を約数にもたないので、1からこれらの数までの整数をすべてかけてできた数の5で割り切れる回数は2012回になります。
以上から、aの値として考えられるものは 8060、8061、8062、8063、8064 で、これが答えです。
簡単な問題です。