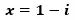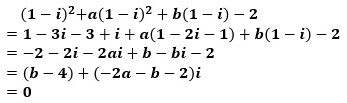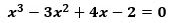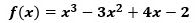こんにちは。東久留米市の学習塾塾長です。
今日が中学の期末試験の最終日で、多くの中学生は夏休みを待つばかりといったところでしょう。その夏休みに旅行を計画している人は多いと思いますが、今回は、「旅行」を表す journey、tour、travel、trip の使い分けです。
「ALL IN ONE」(高山英士著)の傍用問題集 「ENGLISH EX」 には類語の使い分けが取り上げられていて、そのなかの journey、tour、travel、trip の使い分けには、
【journey】
長く困難を伴う旅。陸路の旅を指すことが多い。海路や宇宙の長い旅は voyage と言う。
【tour】
観光[視察]などのために各地を訪問する旅行。
【travel】
旅行。旅行の行為を表す不可算名詞。space travelのように修飾語を伴うことが多い。
【trip】
(米)旅行。出張。遠足・出張のような短いものから長い旅行までを指す。
(英)短い観光旅行。
とあります。(念のため、ウィズダム英和辞典を調べてみたのですがほぼ同じでした)
ということで、「夏休みに北海道へ旅行にいきます」 は、
I’m going on a trip to Hokkaido during the summer vacation.
と trip を使うのがよいでしょう。
今日が中学の期末試験の最終日で、多くの中学生は夏休みを待つばかりといったところでしょう。その夏休みに旅行を計画している人は多いと思いますが、今回は、「旅行」を表す journey、tour、travel、trip の使い分けです。
「ALL IN ONE」(高山英士著)の傍用問題集 「ENGLISH EX」 には類語の使い分けが取り上げられていて、そのなかの journey、tour、travel、trip の使い分けには、
【journey】
長く困難を伴う旅。陸路の旅を指すことが多い。海路や宇宙の長い旅は voyage と言う。
【tour】
観光[視察]などのために各地を訪問する旅行。
【travel】
旅行。旅行の行為を表す不可算名詞。space travelのように修飾語を伴うことが多い。
【trip】
(米)旅行。出張。遠足・出張のような短いものから長い旅行までを指す。
(英)短い観光旅行。
とあります。(念のため、ウィズダム英和辞典を調べてみたのですがほぼ同じでした)
ということで、「夏休みに北海道へ旅行にいきます」 は、
I’m going on a trip to Hokkaido during the summer vacation.
と trip を使うのがよいでしょう。