こんにちは。東久留米市の学習塾塾長です。
今回は、2012年灘高入試に出題された図形問題を取り上げます。
問題は、
「∠Cが直角の直角二等辺三角形ABCがあり、AC=BC=6√2cmである。下図のように、辺AB上に2点P、QをAP=4cm、∠PCQ=45°となるようにとる。

▲問題図
(1) 直線PCに関して点Aと対称な点Dをとる。このとき、△DQC≡△BQCであることを証明せよ。
(2) 線分PQ、BQの長さをそれぞれ求めよ。」
です。
まず図1のように、問題図に与えられた条件を書き入れましょう。

▲図1.与えられた条件を書き入れました
それでは(1)から始めましょう。
直線PCに関して点Aと対称な点Dをとると図2のようになります。

▲図2.点Dを書き入れました
ここから△DQCと△BQCを調べていきましょう。
直線PCは△CADの対称軸なので、
CA=CD [1]
∠ACP=∠DCP [2]
です。
一方、仮定から
CA=CB
なので、これと[1]から
CD=CB [3]
が成り立ちます。
また、
CQは共通 [4]
です。
あとは、∠DCQと∠BCQが等しいことを示せばお仕舞いです。
そこで[2]から
∠ACP=∠DCP=●
とすると、
∠DCQ=∠PCQ-∠PCD
=45°-●
で、
∠BCQ=∠ABC-∠PCQ-∠ACP
=90°-45°-●
=45°-●
になり、これらから
∠DCQ=∠BCQ [5]
が成り立ちます。
[3][4][5]から、2組の辺とその間の角がそれぞれ等しいので、△DQC≡△BQCです。
続いて(2)です。
図3のように、△DQC≡△BQCから∠CDQ=45°です。

▲図3.四角形ACQDは円に内接します
すると∠CDQ=∠CAQ=45°が成り立つので、周角の定理の逆から四角形ACQDは円に内接します。
ここで、直線CPと円との交点をEとすると、直線CEは弦ADの垂直二等分線になるので、線分CEは円の直径になります。
すると∠CAEは半円弧の円周角なので∠CAE=90°になり、∠CAE=∠ACB=90°からAE//CBで、したがって、△PBCと△PAEは相似になります。(図4)
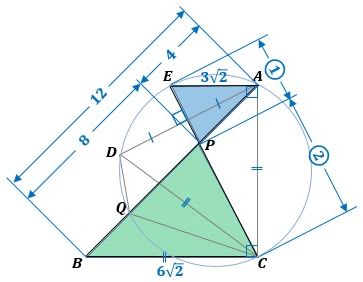
▲図4.△PBC∽△PAEです
ここで、△ABCはAC=6√2cmの直角二等辺三角形なのでAB=12cmです。
このときPB=8cmなので、△PBCと△PAEの相似比は2:1になり、したがって、AE=3√2cmです。
次に図5のように、△PCQと△PAEに注目すると、これらの三角形も相似です。

▲図5.△PCQ∽△PAEです
ここで直角三角形ACEに三平方の定理を適用すると、

から

になり、CP:PE=2:1から
CP=2√10cm
PE=√10cm
です。
すると、PQ:PE=PC:PAから
PQ=√10×2√10/4=5cm
で、さらに、
BQ=BP-PQ=8-5=3cm
です。
以上から、線分PQ、BQの長さは、それぞれ、5cm と 3cm で、これが答えです。
楽しい問題です。
今回は、2012年灘高入試に出題された図形問題を取り上げます。
問題は、
「∠Cが直角の直角二等辺三角形ABCがあり、AC=BC=6√2cmである。下図のように、辺AB上に2点P、QをAP=4cm、∠PCQ=45°となるようにとる。

▲問題図
(1) 直線PCに関して点Aと対称な点Dをとる。このとき、△DQC≡△BQCであることを証明せよ。
(2) 線分PQ、BQの長さをそれぞれ求めよ。」
です。
まず図1のように、問題図に与えられた条件を書き入れましょう。

▲図1.与えられた条件を書き入れました
それでは(1)から始めましょう。
直線PCに関して点Aと対称な点Dをとると図2のようになります。

▲図2.点Dを書き入れました
ここから△DQCと△BQCを調べていきましょう。
直線PCは△CADの対称軸なので、
CA=CD [1]
∠ACP=∠DCP [2]
です。
一方、仮定から
CA=CB
なので、これと[1]から
CD=CB [3]
が成り立ちます。
また、
CQは共通 [4]
です。
あとは、∠DCQと∠BCQが等しいことを示せばお仕舞いです。
そこで[2]から
∠ACP=∠DCP=●
とすると、
∠DCQ=∠PCQ-∠PCD
=45°-●
で、
∠BCQ=∠ABC-∠PCQ-∠ACP
=90°-45°-●
=45°-●
になり、これらから
∠DCQ=∠BCQ [5]
が成り立ちます。
[3][4][5]から、2組の辺とその間の角がそれぞれ等しいので、△DQC≡△BQCです。
続いて(2)です。
図3のように、△DQC≡△BQCから∠CDQ=45°です。

▲図3.四角形ACQDは円に内接します
すると∠CDQ=∠CAQ=45°が成り立つので、周角の定理の逆から四角形ACQDは円に内接します。
ここで、直線CPと円との交点をEとすると、直線CEは弦ADの垂直二等分線になるので、線分CEは円の直径になります。
すると∠CAEは半円弧の円周角なので∠CAE=90°になり、∠CAE=∠ACB=90°からAE//CBで、したがって、△PBCと△PAEは相似になります。(図4)

▲図4.△PBC∽△PAEです
ここで、△ABCはAC=6√2cmの直角二等辺三角形なのでAB=12cmです。
このときPB=8cmなので、△PBCと△PAEの相似比は2:1になり、したがって、AE=3√2cmです。
次に図5のように、△PCQと△PAEに注目すると、これらの三角形も相似です。

▲図5.△PCQ∽△PAEです
ここで直角三角形ACEに三平方の定理を適用すると、

から

になり、CP:PE=2:1から
CP=2√10cm
PE=√10cm
です。
すると、PQ:PE=PC:PAから
PQ=√10×2√10/4=5cm
で、さらに、
BQ=BP-PQ=8-5=3cm
です。
以上から、線分PQ、BQの長さは、それぞれ、5cm と 3cm で、これが答えです。
楽しい問題です。










