こんにちは。東久留米市の学習塾塾長です。
今回は平成30年度都立高校数学入試問題を取り上げます。
問題は、国立高で出題された大問3の図形問題で、それは、
「下の図1で、点Oは線分ABを直径とする半円の中心である。
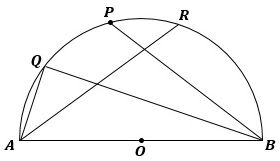
▲図1.問題図(1)
点Pは弧AB上にある点で、点Aと点Bのいずれにも一致しない。
点Bと点Pを結ぶ。
ただし、∠ABPは60°以下の角とする。
∠ABPの二等分線と弧APの交点をQとする。
点Aと点Qを結び、∠BAQの二等分線と弧BQの交点をRとする。
次の各問に答えよ。
[問1] 弧BR:弧RP=2:1 のとき、∠ABPの大きさは何度か。
[問2] 下の図2は、図1において、点Qから線分ABに垂直な直線を引き、その交点をH、線分ARと線分QHの交点を I、線分ARと線分BQの交点をJとした場合を表している。

▲図2.問題図(2)
(1) QI=QJ であることを証明せよ。
(2) OA=1cmとする。
∠ABP=60°のとき、線分IJの長さは何cmか。」
です。
[問1]です。
図3のように、与えられた条件を書き入れましょう。

▲図3.与えられた条件を書き入れました
図4のように点Aと点Pを結ぶと、∠APBは半円弧に対する円周角なので、∠APB=90°で、同様に、∠AQB=90°になります。

▲図4.∠APB=∠AQB=90°です
ここで、∠ABQ=∠QBP=●、∠BAR=∠RAQ=■とします。
すると、弧BR:弧RP=2:1から、∠PAR=■/2です。
直角三角形ABPの内角に注目すると、
2●+3■/2+90°=180° → 8●+6■=360°
が成り立ち、さらに直角三角形ABQの内角に注目すると、
●+2■+90°=180° → 3●+6■=270°
が成り立ちます。
これら2式から
5●=90° → ●=18°
になり、∠ABP=2●から
∠ABP=18°×2=36°
で、これが答えです。
次に[問2]の(1)です。
QI=QJを示すには、∠QIJ=∠QJIを示すのがよいでしょう。
そこで図5のように、点Bと点Rを結び、∠QBR=●とします。

▲図5.∠QBR=●としました
このとき、∠BRJ=∠BRA=90°ですから、直角三角形BRIの内角に注目して、
∠BJR=180°-∠BRJ-∠QBR=90°-●
で、∠QJIと∠BJRは対頂角の関係なので、
∠QJI=90°-● [1]
が成り立ちます。
一方、円周角の定理から
∠QBR=∠QAR
で、仮定から
∠QAR=∠BAR
です。
したがって、∠BAR=∠HAI=●になります。
ここで、直角三角形AHIの内角に注目すると、
∠AIH=180°-∠AHI-∠HAI=90°-●
で、∠QIJと∠AIHは対頂角の関係なので、
∠QIJ=90°-● [2]
が成り立ちます。
[1]と[2]から、∠QJI=∠QIJが成り立ち、2つの内角が等しい三角形は二等辺三角形なので、QI=QJです。
最後の[問2](2)です。
∠ABP=60°から∠BAP=30°です。
一方、∠ABQ=30°から∠BAQ=60°で、したがって、∠BAR=30°になります。
以上から、図6のように、点Pと点Rは同じ点になります。

▲図6.点Pと点Rは同じ点です
このとき、△AHI、△BPJは内角が90°、60°、30°の直角三角形なので、∠AIH=∠BJR=60°で、△QIJは正三角形です。
一方、△ABP≡△BAQからBP=AQで、したがって、△BPJ≡△AQJになるので、
IJ=QJ=PJ (★)
です。
ここで、直角三角形ABPに注目すると、
AB:BP:AP=2:1:√3
で、AB=2cmですから、
BP=1cm
AP=√3cm
です。
次に、直角三角形BPJに注目すると、
BP:PJ=√3:1
で、BP=1cmですから、
PJ=1/√3=√3/3cm
です。
すると(★)から、
IJ=√3/3 cm
で、これが答えです。
簡単な問題です。
今回は平成30年度都立高校数学入試問題を取り上げます。
問題は、国立高で出題された大問3の図形問題で、それは、
「下の図1で、点Oは線分ABを直径とする半円の中心である。

▲図1.問題図(1)
点Pは弧AB上にある点で、点Aと点Bのいずれにも一致しない。
点Bと点Pを結ぶ。
ただし、∠ABPは60°以下の角とする。
∠ABPの二等分線と弧APの交点をQとする。
点Aと点Qを結び、∠BAQの二等分線と弧BQの交点をRとする。
次の各問に答えよ。
[問1] 弧BR:弧RP=2:1 のとき、∠ABPの大きさは何度か。
[問2] 下の図2は、図1において、点Qから線分ABに垂直な直線を引き、その交点をH、線分ARと線分QHの交点を I、線分ARと線分BQの交点をJとした場合を表している。

▲図2.問題図(2)
(1) QI=QJ であることを証明せよ。
(2) OA=1cmとする。
∠ABP=60°のとき、線分IJの長さは何cmか。」
です。
[問1]です。
図3のように、与えられた条件を書き入れましょう。

▲図3.与えられた条件を書き入れました
図4のように点Aと点Pを結ぶと、∠APBは半円弧に対する円周角なので、∠APB=90°で、同様に、∠AQB=90°になります。

▲図4.∠APB=∠AQB=90°です
ここで、∠ABQ=∠QBP=●、∠BAR=∠RAQ=■とします。
すると、弧BR:弧RP=2:1から、∠PAR=■/2です。
直角三角形ABPの内角に注目すると、
2●+3■/2+90°=180° → 8●+6■=360°
が成り立ち、さらに直角三角形ABQの内角に注目すると、
●+2■+90°=180° → 3●+6■=270°
が成り立ちます。
これら2式から
5●=90° → ●=18°
になり、∠ABP=2●から
∠ABP=18°×2=36°
で、これが答えです。
次に[問2]の(1)です。
QI=QJを示すには、∠QIJ=∠QJIを示すのがよいでしょう。
そこで図5のように、点Bと点Rを結び、∠QBR=●とします。

▲図5.∠QBR=●としました
このとき、∠BRJ=∠BRA=90°ですから、直角三角形BRIの内角に注目して、
∠BJR=180°-∠BRJ-∠QBR=90°-●
で、∠QJIと∠BJRは対頂角の関係なので、
∠QJI=90°-● [1]
が成り立ちます。
一方、円周角の定理から
∠QBR=∠QAR
で、仮定から
∠QAR=∠BAR
です。
したがって、∠BAR=∠HAI=●になります。
ここで、直角三角形AHIの内角に注目すると、
∠AIH=180°-∠AHI-∠HAI=90°-●
で、∠QIJと∠AIHは対頂角の関係なので、
∠QIJ=90°-● [2]
が成り立ちます。
[1]と[2]から、∠QJI=∠QIJが成り立ち、2つの内角が等しい三角形は二等辺三角形なので、QI=QJです。
最後の[問2](2)です。
∠ABP=60°から∠BAP=30°です。
一方、∠ABQ=30°から∠BAQ=60°で、したがって、∠BAR=30°になります。
以上から、図6のように、点Pと点Rは同じ点になります。

▲図6.点Pと点Rは同じ点です
このとき、△AHI、△BPJは内角が90°、60°、30°の直角三角形なので、∠AIH=∠BJR=60°で、△QIJは正三角形です。
一方、△ABP≡△BAQからBP=AQで、したがって、△BPJ≡△AQJになるので、
IJ=QJ=PJ (★)
です。
ここで、直角三角形ABPに注目すると、
AB:BP:AP=2:1:√3
で、AB=2cmですから、
BP=1cm
AP=√3cm
です。
次に、直角三角形BPJに注目すると、
BP:PJ=√3:1
で、BP=1cmですから、
PJ=1/√3=√3/3cm
です。
すると(★)から、
IJ=√3/3 cm
で、これが答えです。
簡単な問題です。










