こんにちは。東久留米市の学習塾塾長です。
今回は、2013年灘高入試に出題された面積問題を取り上げます。
問題は、
「長方形ABCDの辺BC、CD、DA上にそれぞれ点E、F、Gをとり、線分EC上に点Hをとると下図のようになり、四角形ABEG、HECFはともに正方形となった。次の問いに答えよ。なお、答えが複数ある場合は、それらをすべて答えること。

▲問題図
(1) 長方形ABCDの面積が長方形GHFDの面積の6倍であるとき、BE:EC をできるだけ簡単な整数の比で表せ。
(2) △ABCの面積が6、△FDGの面積が1であるとき、正方形ABEGの面積を求めよ。」
です。
(1)から取り掛かりましょう。
図1のように、AE=x、EC=yとすると、
(長方形ABCDの面積)=x(x+y)
(長方形GHFDの面積)=(x-y)y
で、与えられた条件から、
x(x+y)=6(x-y)y
が成り立ちます。

▲図1.AE=x、EC=y としました
これを展開・整理して、

とします。
ここで、さらに因数分解すると、
(x-2y)(x-3y)=0
になり、
x=2y または、3y
です。
これから
x:y=2:1、または、3:1
になり、したがって、BE:EC= 2:1、または、3:1 で、これが答えです。
続いて(2)です。
図2に与えられた条件を書き入れました。
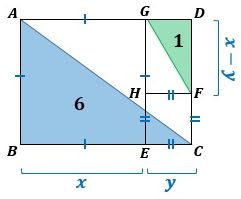
▲図2.与えられた条件を書き入れました
△ABCの面積と△FDGの面積がそれぞれ6と1なので、長方形ABCDの面積は長方形GHFDの面積の6倍になり、(1)の結果から、
x=2y、または、3y
が成り立ちます。
一方、
(△ABCの面積)=x(x+y)/2=6
から、

が成り立ちます。
● x=2yの場合

から

● x=3yの場合

から

です。
したがって、正方形ABEGの面積は 8、または、9 で、これが答えです。
△ABCと△FDGの面積をx、yで表して、その連立2次方程式を解いてもOKです。
今回は、2013年灘高入試に出題された面積問題を取り上げます。
問題は、
「長方形ABCDの辺BC、CD、DA上にそれぞれ点E、F、Gをとり、線分EC上に点Hをとると下図のようになり、四角形ABEG、HECFはともに正方形となった。次の問いに答えよ。なお、答えが複数ある場合は、それらをすべて答えること。

▲問題図
(1) 長方形ABCDの面積が長方形GHFDの面積の6倍であるとき、BE:EC をできるだけ簡単な整数の比で表せ。
(2) △ABCの面積が6、△FDGの面積が1であるとき、正方形ABEGの面積を求めよ。」
です。
(1)から取り掛かりましょう。
図1のように、AE=x、EC=yとすると、
(長方形ABCDの面積)=x(x+y)
(長方形GHFDの面積)=(x-y)y
で、与えられた条件から、
x(x+y)=6(x-y)y
が成り立ちます。

▲図1.AE=x、EC=y としました
これを展開・整理して、

とします。
ここで、さらに因数分解すると、
(x-2y)(x-3y)=0
になり、
x=2y または、3y
です。
これから
x:y=2:1、または、3:1
になり、したがって、BE:EC= 2:1、または、3:1 で、これが答えです。
続いて(2)です。
図2に与えられた条件を書き入れました。

▲図2.与えられた条件を書き入れました
△ABCの面積と△FDGの面積がそれぞれ6と1なので、長方形ABCDの面積は長方形GHFDの面積の6倍になり、(1)の結果から、
x=2y、または、3y
が成り立ちます。
一方、
(△ABCの面積)=x(x+y)/2=6
から、

が成り立ちます。
● x=2yの場合

から

● x=3yの場合

から

です。
したがって、正方形ABEGの面積は 8、または、9 で、これが答えです。
△ABCと△FDGの面積をx、yで表して、その連立2次方程式を解いてもOKです。










