こんにちは。東久留米市の学習塾塾長です。
今回は、2017年灘高入試に出題された場合の数の問題を取り上げます。
問題は、
「A、B、C、Dの4人が、a、b、c、d、e、f、g の7冊の本からそれぞれ3冊を選んで読む。ただし、どの2人についても共通に読む本が1冊だけあるようにする。
(1) A、B、Cの3人について共通に読む本が1冊だけあり、Dはその本を読まないような、4人の本の選び方は何通りあるか。
(2) 4人のうちどの3人についても共通に読む本がないような、4人の本の選び方は何通りあるか。
(3) 4人の本の選び方は全部で何通りあるか。」
です。
(1)から取り掛かりましょう。
表1のように、A、B、Cが共通して読む本を本1とします。
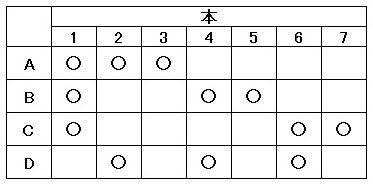
▲表1.A、B、Cが共通して読む本を本1としました
さらにAが本2と3を読んだとすると、BとCは本2、3を読むことができないので、BとCが読む本をそれぞれ本4、5と本6、7とします。
このとき、Dが本2、4、6を読めば、どの2人についても共通に読む本が1冊だけあるようにすることができます。
ここで本1から7に、aからgを対応させる場合の数は、
7×6×5×4×3×2×1= 5040 (通り)
で、これが答えです。
次に(2)です。
表2のように、AとB、AとC、AとDが共通して読む本をそれぞれ本1、2、3とします。

▲表2.AとB、AとC、AとDが共通して読む本をそれぞれ本1、2、3としました
さらにBとC、BとD、CとDが共通して読む本をそれぞれ本4、5、6とすると、どの2人についても共通に読む本が1冊だけあり、かつ、どの3人についても共通に読む本がないようにすることができます。
ここで本1から7に、aからgを対応させる場合の数は、
7×6×5×4×3×2×1= 5040 (通り)
で、これが答えです。
最後の(3)です。
どの2人についても共通に読む本が1冊だけあるようになるのは、
[1](1)のように、3人が共通する本を読む
[2](2)のように、2人が共通する本を読む
[3]4人が共通する本を読む
のいずれかの場合です。
[1]の場合の数は、(1)でのDの選び方が4通りあるので、
5040×4=20160(通り)
です。
[2]の場合の数は、(2)から
5040(通り)
です。
[3]の場合は、表3のように、本が9冊必要になり条件を満たすことはできません。

▲表3.4人が共通する本を読むと、本は9冊必要です
したがって、4人の本の選び方は、
20160+5040= 25200 (通り)
で、これが答えです。
楽しい問題です。
今回は、2017年灘高入試に出題された場合の数の問題を取り上げます。
問題は、
「A、B、C、Dの4人が、a、b、c、d、e、f、g の7冊の本からそれぞれ3冊を選んで読む。ただし、どの2人についても共通に読む本が1冊だけあるようにする。
(1) A、B、Cの3人について共通に読む本が1冊だけあり、Dはその本を読まないような、4人の本の選び方は何通りあるか。
(2) 4人のうちどの3人についても共通に読む本がないような、4人の本の選び方は何通りあるか。
(3) 4人の本の選び方は全部で何通りあるか。」
です。
(1)から取り掛かりましょう。
表1のように、A、B、Cが共通して読む本を本1とします。

▲表1.A、B、Cが共通して読む本を本1としました
さらにAが本2と3を読んだとすると、BとCは本2、3を読むことができないので、BとCが読む本をそれぞれ本4、5と本6、7とします。
このとき、Dが本2、4、6を読めば、どの2人についても共通に読む本が1冊だけあるようにすることができます。
ここで本1から7に、aからgを対応させる場合の数は、
7×6×5×4×3×2×1= 5040 (通り)
で、これが答えです。
次に(2)です。
表2のように、AとB、AとC、AとDが共通して読む本をそれぞれ本1、2、3とします。

▲表2.AとB、AとC、AとDが共通して読む本をそれぞれ本1、2、3としました
さらにBとC、BとD、CとDが共通して読む本をそれぞれ本4、5、6とすると、どの2人についても共通に読む本が1冊だけあり、かつ、どの3人についても共通に読む本がないようにすることができます。
ここで本1から7に、aからgを対応させる場合の数は、
7×6×5×4×3×2×1= 5040 (通り)
で、これが答えです。
最後の(3)です。
どの2人についても共通に読む本が1冊だけあるようになるのは、
[1](1)のように、3人が共通する本を読む
[2](2)のように、2人が共通する本を読む
[3]4人が共通する本を読む
のいずれかの場合です。
[1]の場合の数は、(1)でのDの選び方が4通りあるので、
5040×4=20160(通り)
です。
[2]の場合の数は、(2)から
5040(通り)
です。
[3]の場合は、表3のように、本が9冊必要になり条件を満たすことはできません。

▲表3.4人が共通する本を読むと、本は9冊必要です
したがって、4人の本の選び方は、
20160+5040= 25200 (通り)
で、これが答えです。
楽しい問題です。










