こんにちは。東久留米市の学習塾塾長です。
今回は平成30年度都立高校数学入試問題を取り上げます。
問題は、共通問題で出題された大問4の図形問題で、それは、
「下の図1で、点Oは線分ABを直径とする円の中心である。

▲図1.問題図(1)
点Cは円Oの周上にある点で、弧AC=弧BCである。
点Pは、点Cを含まない弧AB上にある点で、点A、点Bのいずれにも一致しない。
点Aと点C、点Cと点Pをそれぞれ結び、線分ABと線分CPとの交点をQとする。
次の各問に答えよ。
[問1] 図1において、∠ACP=a° とするとき、∠AQPの大きさを表す式を、次のア~エのうちから選び、記号で答えよ。
ア (60-a)度 イ (90-a)度 ウ (a+30)度 エ (a+45)度
[問2] 下の図2は、図1において、点Aと点P、点Bと点Pをそれぞれ結び、線分BPをPの方向に延ばした直線上にありBP=RPとなる点をRとし、点Aと点Rを結んだ場合を表している。

▲図2.問題図(2)
次の①、②に答えよ。
① △ABP≡△ARPであることを証明せよ。
② 次の[ ]の中の「か」「き」に当てはまる数字をそれぞれ答えよ。
図2において、点Oと点Pを結んだ場合を考える。
弧BC=2×弧BPのとき、
△ACQの面積は、四角形AOPRの面積の[ か ]/[ き ]倍である。」
です。
[問1]です。
図3のように、与えられた条件を図1に書き入れましょう。

▲図3.与えられた条件を図1に書き入れました
図4のように、弧AC=弧BCから∠AOC=90°なので、△OACは直角二等辺三角形になります。
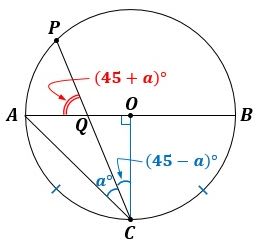
▲図4.△OACは直角二等辺三角形です
つまり、∠OCA=45°で、これから∠OCQ=(45-a)°です。
ここで△OCQの内角に注目すると、∠OQC=180°-90°-(45-a)°=(45+a)°で、∠AQPと∠OQCは対頂角でひとしいので、∠AQP=(45+a)°です。
したがって、エ が答えです。
続いて[問2]の①です。
図5のように、与えられた条件を図2に書き入れましょう。
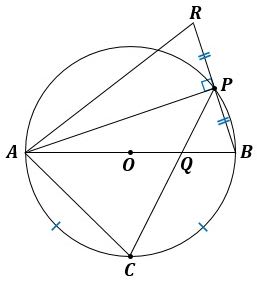
▲図5.与えられた条件を図2に書き入れました
図5で、∠APBは半円弧ACBに対する円周角なので、∠APB=90°です。
すると、△ABPと△ARPはどちらも直角三角形で∠APB=∠APR=90°になり、さらに、BP=RP(仮定)、APは共通から、2組の辺とその間の角がそれぞれ等しいので、△ABP≡△ARPです。
最後の②です。
図6のように、△ACQ(赤色でマークしました)と四角形AOPR(緑色でマークしました)の面積を計算するのですが、いくつかの相似三角形があって、どれを選ぶか迷うところです。

▲図6.△ACQ(赤色でマーク)と四角形AOPR(緑色でマーク)です
ここでは図7のように、△ACQ(赤色でマーク)と△OBP(緑色でマーク)を選ぶのが簡単そうです。

▲図7.△ACQ(赤色でマーク)と△OBP(緑色でマーク)を選びます
弧BCは円周の1/4なので、その中心角∠BOC=90°、円周角∠BAC=45°です。
また弧BC=2×弧BPから、弧BPに対する中心角∠BOP=45°になります。
したがって、∠BAC=∠BOPです。
一方、∠ACPと∠ABPは弧AP(点B、Cを含まない方)の円周角なので、∠ACP=∠ABPで、∠ACP=∠ACQ、∠ABP=∠OBPから、∠ACQ=∠OBPです。
以上から、△ACQ∽△OBPであることが判りました。
そこで、これらの相似比を計算しましょう。
図8のように、円Oの半径をrとすると、AC=√2rで、AC:OB=√2r:r=√2:1です。

▲図8.円Oの半径をrとしました
つまり、
(△ACQの面積):(△OBPの面積)=2:1 (1)
になります。
次に、△BOPと△BARに注目すると、BO:BA=BP:BR=1:2、∠Bは共通から、△BOP∽△BARで、相似比は1:2です。
つまり、(△BOPの面積):(△BARの面積)=1:4で、このとき、(四角形AOPRの面積)=(△BARの面積)-(△OBPの面積)なので、
(△OBPの面積):(四角形AOPRの面積)=1:3 (2)
です。
すると(1)と(2)から、
(△ACQの面積):(四角形AOPRの面積)=2:3
になります。
したがって、[ か ]=2、[ き ]=3 で、これが答えです。
[問2]の②では、異なる組合せの相似三角形を選んでもOKですが、少し煩雑になりそうです。
今回は平成30年度都立高校数学入試問題を取り上げます。
問題は、共通問題で出題された大問4の図形問題で、それは、
「下の図1で、点Oは線分ABを直径とする円の中心である。

▲図1.問題図(1)
点Cは円Oの周上にある点で、弧AC=弧BCである。
点Pは、点Cを含まない弧AB上にある点で、点A、点Bのいずれにも一致しない。
点Aと点C、点Cと点Pをそれぞれ結び、線分ABと線分CPとの交点をQとする。
次の各問に答えよ。
[問1] 図1において、∠ACP=a° とするとき、∠AQPの大きさを表す式を、次のア~エのうちから選び、記号で答えよ。
ア (60-a)度 イ (90-a)度 ウ (a+30)度 エ (a+45)度
[問2] 下の図2は、図1において、点Aと点P、点Bと点Pをそれぞれ結び、線分BPをPの方向に延ばした直線上にありBP=RPとなる点をRとし、点Aと点Rを結んだ場合を表している。

▲図2.問題図(2)
次の①、②に答えよ。
① △ABP≡△ARPであることを証明せよ。
② 次の[ ]の中の「か」「き」に当てはまる数字をそれぞれ答えよ。
図2において、点Oと点Pを結んだ場合を考える。
弧BC=2×弧BPのとき、
△ACQの面積は、四角形AOPRの面積の[ か ]/[ き ]倍である。」
です。
[問1]です。
図3のように、与えられた条件を図1に書き入れましょう。

▲図3.与えられた条件を図1に書き入れました
図4のように、弧AC=弧BCから∠AOC=90°なので、△OACは直角二等辺三角形になります。

▲図4.△OACは直角二等辺三角形です
つまり、∠OCA=45°で、これから∠OCQ=(45-a)°です。
ここで△OCQの内角に注目すると、∠OQC=180°-90°-(45-a)°=(45+a)°で、∠AQPと∠OQCは対頂角でひとしいので、∠AQP=(45+a)°です。
したがって、エ が答えです。
続いて[問2]の①です。
図5のように、与えられた条件を図2に書き入れましょう。

▲図5.与えられた条件を図2に書き入れました
図5で、∠APBは半円弧ACBに対する円周角なので、∠APB=90°です。
すると、△ABPと△ARPはどちらも直角三角形で∠APB=∠APR=90°になり、さらに、BP=RP(仮定)、APは共通から、2組の辺とその間の角がそれぞれ等しいので、△ABP≡△ARPです。
最後の②です。
図6のように、△ACQ(赤色でマークしました)と四角形AOPR(緑色でマークしました)の面積を計算するのですが、いくつかの相似三角形があって、どれを選ぶか迷うところです。

▲図6.△ACQ(赤色でマーク)と四角形AOPR(緑色でマーク)です
ここでは図7のように、△ACQ(赤色でマーク)と△OBP(緑色でマーク)を選ぶのが簡単そうです。

▲図7.△ACQ(赤色でマーク)と△OBP(緑色でマーク)を選びます
弧BCは円周の1/4なので、その中心角∠BOC=90°、円周角∠BAC=45°です。
また弧BC=2×弧BPから、弧BPに対する中心角∠BOP=45°になります。
したがって、∠BAC=∠BOPです。
一方、∠ACPと∠ABPは弧AP(点B、Cを含まない方)の円周角なので、∠ACP=∠ABPで、∠ACP=∠ACQ、∠ABP=∠OBPから、∠ACQ=∠OBPです。
以上から、△ACQ∽△OBPであることが判りました。
そこで、これらの相似比を計算しましょう。
図8のように、円Oの半径をrとすると、AC=√2rで、AC:OB=√2r:r=√2:1です。

▲図8.円Oの半径をrとしました
つまり、
(△ACQの面積):(△OBPの面積)=2:1 (1)
になります。
次に、△BOPと△BARに注目すると、BO:BA=BP:BR=1:2、∠Bは共通から、△BOP∽△BARで、相似比は1:2です。
つまり、(△BOPの面積):(△BARの面積)=1:4で、このとき、(四角形AOPRの面積)=(△BARの面積)-(△OBPの面積)なので、
(△OBPの面積):(四角形AOPRの面積)=1:3 (2)
です。
すると(1)と(2)から、
(△ACQの面積):(四角形AOPRの面積)=2:3
になります。
したがって、[ か ]=2、[ き ]=3 で、これが答えです。
[問2]の②では、異なる組合せの相似三角形を選んでもOKですが、少し煩雑になりそうです。










