図のように円周を6等分する6つの点がある。この6つの点から無作為に選んだ3つの点を頂点とする三角形をつくるとき、その三角形が直角三角形になる確率はいくらか。1〜5から一つ選べ。
三角形は何個できるかというと、6つの点から3つの点を選ぶ組み合わせなので、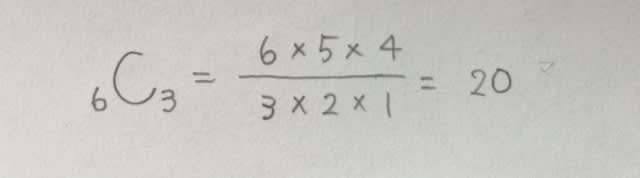
20個の三角形ができます。そのうち、直角三角形は何個あるでしょうか?直径に対する円周角は90°なので、例えば、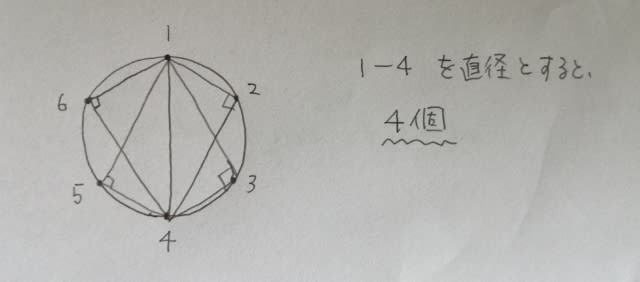
同様に、2ー5を直径としたときも4個、3ー6を直径としたときも4個あるので、全部で4×3=12個ありますね。よって、
正解は、肢3です。ここをポチッとお願いします。→
にほんブログ村


三角形は何個できるかというと、6つの点から3つの点を選ぶ組み合わせなので、
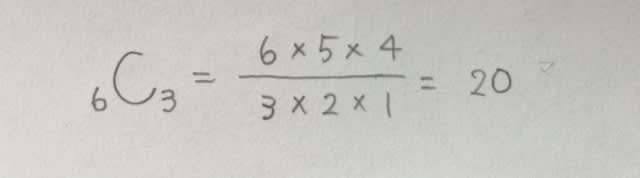
20個の三角形ができます。そのうち、直角三角形は何個あるでしょうか?直径に対する円周角は90°なので、例えば、

同様に、2ー5を直径としたときも4個、3ー6を直径としたときも4個あるので、全部で4×3=12個ありますね。よって、

正解は、肢3です。ここをポチッとお願いします。→
にほんブログ村






















※コメント投稿者のブログIDはブログ作成者のみに通知されます