次の図のように床にマス目があり、そこに1から9までの数字が書かれている。A、B、C、D、Eの5人が好きな数字の上に立ち、前を向いている。1マスには1人しか入れない。A~Eの5人がそれぞれの立ち位置に関して次のように述べているとき、人が立っていないマスに書かれた数の合計として正しいのはどれか。 A 「私は全体の中央にいる。」 B 「私の左右には両方人がいる。」 C 「私がいるところの数は3の倍数である。」 D 「私がいるのはAをはさんでちょうどCの反対側である。」 E 「私がいるところの数で他の人のいるところの数を割った値はすべて整数である。」①16②21③24④27⑤30 条件を見ていくと、
A 「私は全体の中央にいる。」 B 「私の左右には両方人がいる。」 C 「私がいるところの数は3の倍数である。」 D 「私がいるのはAをはさんでちょうどCの反対側である。」 E 「私がいるところの数で他の人のいるところの数を割った値はすべて整数である。」①16②21③24④27⑤30 条件を見ていくと、 仮に、Eが2だとしたらどうでしょうか?E以外の4人は、4、6、8、10。10はダメですね。Eが3以上だとしたら、もっとダメです。よって、Eは1にいます。
仮に、Eが2だとしたらどうでしょうか?E以外の4人は、4、6、8、10。10はダメですね。Eが3以上だとしたら、もっとダメです。よって、Eは1にいます。 次に、Cが6だったらどうでしょうか?Dの発言も考えると、
次に、Cが6だったらどうでしょうか?Dの発言も考えると、 Cが9だとしても、
Cが9だとしても、 よって、Cは3にいます。ということは、Dは7にいて、Bは2にいることになります。
よって、Cは3にいます。ということは、Dは7にいて、Bは2にいることになります。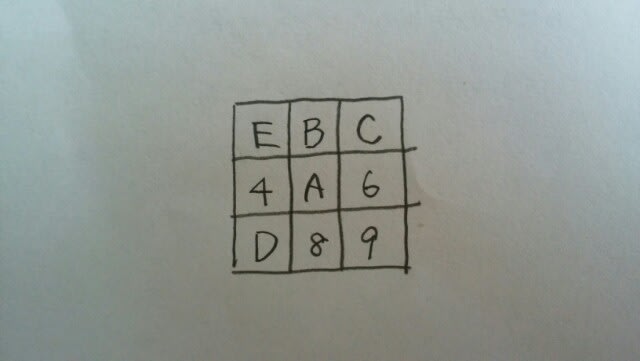 人が立っていないマスに書かれた数の合計は、4+6+8+9=27なので、正解は肢④です。
人が立っていないマスに書かれた数の合計は、4+6+8+9=27なので、正解は肢④です。

 A 「私は全体の中央にいる。」 B 「私の左右には両方人がいる。」 C 「私がいるところの数は3の倍数である。」 D 「私がいるのはAをはさんでちょうどCの反対側である。」 E 「私がいるところの数で他の人のいるところの数を割った値はすべて整数である。」①16②21③24④27⑤30 条件を見ていくと、
A 「私は全体の中央にいる。」 B 「私の左右には両方人がいる。」 C 「私がいるところの数は3の倍数である。」 D 「私がいるのはAをはさんでちょうどCの反対側である。」 E 「私がいるところの数で他の人のいるところの数を割った値はすべて整数である。」①16②21③24④27⑤30 条件を見ていくと、 仮に、Eが2だとしたらどうでしょうか?E以外の4人は、4、6、8、10。10はダメですね。Eが3以上だとしたら、もっとダメです。よって、Eは1にいます。
仮に、Eが2だとしたらどうでしょうか?E以外の4人は、4、6、8、10。10はダメですね。Eが3以上だとしたら、もっとダメです。よって、Eは1にいます。 次に、Cが6だったらどうでしょうか?Dの発言も考えると、
次に、Cが6だったらどうでしょうか?Dの発言も考えると、 Cが9だとしても、
Cが9だとしても、 よって、Cは3にいます。ということは、Dは7にいて、Bは2にいることになります。
よって、Cは3にいます。ということは、Dは7にいて、Bは2にいることになります。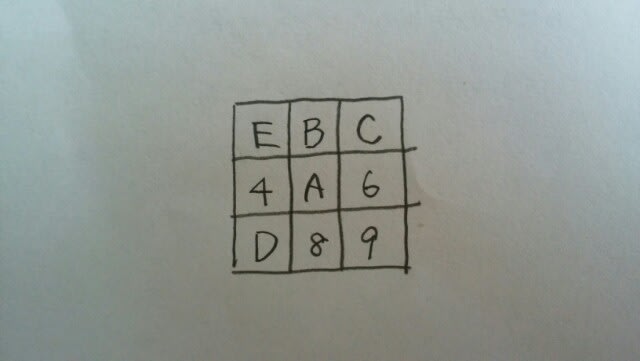 人が立っていないマスに書かれた数の合計は、4+6+8+9=27なので、正解は肢④です。
人が立っていないマスに書かれた数の合計は、4+6+8+9=27なので、正解は肢④です。











 ○Aは男子で、真向かいには図書委員が座っていた。 ○Bは生活委員で、両隣にはEとFが座っていた。 ○Cは女子で、隣には図書委員が座っていた。 ○Dの右隣には、Aが座っていた。 ○環境委員の隣には、学級委員の男子が座っていた。 ○学級委員の真向かいには、給食委員が座っていた。 ①Aは環境委員で、Aの右隣にはEが座っていた。 ②Cは給食委員で、Cの右隣にはDが座っていた。 ③Dは体育委員で、真向かいにはFが座っていた。 ④Eは学級委員で、Eの左隣にはAが座っていた。 ⑤Fは図書委員で、Fの左隣にはBが座っていた。 こういう問題では、まず、「左隣」、「右隣」という条件からみていくのが手筋です。
○Aは男子で、真向かいには図書委員が座っていた。 ○Bは生活委員で、両隣にはEとFが座っていた。 ○Cは女子で、隣には図書委員が座っていた。 ○Dの右隣には、Aが座っていた。 ○環境委員の隣には、学級委員の男子が座っていた。 ○学級委員の真向かいには、給食委員が座っていた。 ①Aは環境委員で、Aの右隣にはEが座っていた。 ②Cは給食委員で、Cの右隣にはDが座っていた。 ③Dは体育委員で、真向かいにはFが座っていた。 ④Eは学級委員で、Eの左隣にはAが座っていた。 ⑤Fは図書委員で、Fの左隣にはBが座っていた。 こういう問題では、まず、「左隣」、「右隣」という条件からみていくのが手筋です。


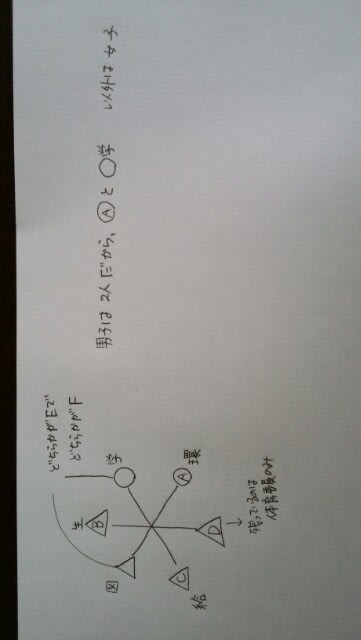 ①Aは確かに環境委員ですが、右隣はEかFか、分かりません。②正しい。③Dは確かに体育委員ですが、向かいにはBが座っています。④学級委員は、EかFか、分かりません。⑤図書委員は、EかFか、分かりません。正解は、②です。ここまで考えると、何となく、あることに気がついてきます。究極、この問題は、次のように考えると、すぐに答が出ます。
①Aは確かに環境委員ですが、右隣はEかFか、分かりません。②正しい。③Dは確かに体育委員ですが、向かいにはBが座っています。④学級委員は、EかFか、分かりません。⑤図書委員は、EかFか、分かりません。正解は、②です。ここまで考えると、何となく、あることに気がついてきます。究極、この問題は、次のように考えると、すぐに答が出ます。


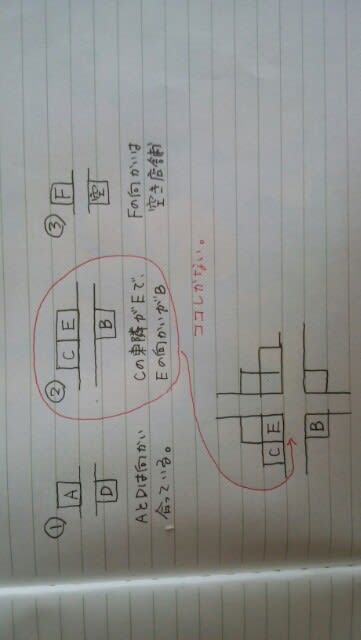 実は、これでもう正解が出ています。Bのお店には、隣などないのだから、肢1、肢2、肢3いずれもダメ。Fの発言より、空き店舗の一つはFのお店と向かいあっているのですから、肢5もダメ。肢4しか正解はありません。肢4が正しいのは、以下の理由です。
実は、これでもう正解が出ています。Bのお店には、隣などないのだから、肢1、肢2、肢3いずれもダメ。Fの発言より、空き店舗の一つはFのお店と向かいあっているのですから、肢5もダメ。肢4しか正解はありません。肢4が正しいのは、以下の理由です。