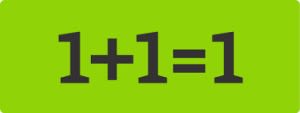
4月バカのきょうは、ありえない嘘にだまされてみるのも一興(一驚)と思い話題提供します。
次に従って、1+1が 2にならず、どのように考えれば 1になるかをお試しください。
どこにトリックがあるのでしょうか、果たしてこのパラドックスの仕掛けをみつけられるでしょうか ?
X = 1
のとき
両辺にXをかけても良く
X2=X
両辺から1を引いても良いので
X2-1=X-1
これを 因数分解すると
(X+1)(X-1)=X-1
両辺を X-1 で 割ると
X+1=1
X=1 なのだから
この式に X=1 を 代入すると
ほら
1+1=1
クリック



次に従って、1+1が 2にならず、どのように考えれば 1になるかをお試しください。
どこにトリックがあるのでしょうか、果たしてこのパラドックスの仕掛けをみつけられるでしょうか ?
X = 1
のとき
両辺にXをかけても良く
X2=X
両辺から1を引いても良いので
X2-1=X-1
これを 因数分解すると
(X+1)(X-1)=X-1
両辺を X-1 で 割ると
X+1=1
X=1 なのだから
この式に X=1 を 代入すると
ほら
1+1=1
クリック




















正三角形の二編の長さは一辺の長さに等しいか?
答え、等しい!なぜか証明せよ・・・・。
これはまた、「しじゅうから交響楽談」に書きます、お楽しみに!
解答集見たけど、みんな頭いいね~。
数学苦手だったからチンプンカンプンでした。
どーしても
「Xの二乗=X」
の時点で納得がいかん、とそこで思考がストップしておりました(笑)。
そのうちキレて
「X=1って、もうすでに分かってるんだから、
その後Xを使っていくのがおかしいだろって
投げ出しちゃいました。
A=マツダ とする
被害者を殺害した少年Aは……。
ほら、バカみたいな文章でしょ?
中学まで数学は一番の得意科目だったのですが、
今ではすっかり・・・
「なるほど~。ふむふむ・・・考えた人はすごいなぁ。」
と思いながら、自分でもやってみました。
ほんと、考えた人すごいなぁ・・・
私は数学が最も苦手な教科だったので
全然わかりませんですぅ・・・。
解答集、私も見ましたが皆さん凄いです!
ように、(1+1)×0=0の両辺を0で約分したからですよね。
X-1=0ですから。
最初にX=1と定義していますから、X-1=0です。これで辺々を割っているので、ここがトリックです。
ではでは、失礼いたしました♪
パラドックスですかぁ
ここに答え書いても良いのかなぁ?
> X+1=1
> X=1 なのだから
ここでXに1を代入してるのが矛盾の元ですね
ここでのXは何でも好きな値の入れられる変数ではなく
あくまでもX+1=1となる値のみを取れるという条件付の変数なので、
ここに1をいれた事で矛盾というか間違いが起きています
もし、あってて不都合だったら消しちゃってください(=゜ω゜)ノ
あまり数学は得意なほうではないのですが何度か読んだところで分かりました。
でもそれでいくとina+Xでも答えは1ってことになりますかね。実際にはおそらくもう少しいい結果になっていると思います。