(山登りの話ではないが、普段お世話になってる地図に関する事だから、記事にしてみました。)
ひょんな事から、メルカトル図法に大きな興味を持った。
”メルカトル図法”と言えば、誰でも一度は聞いたことはあると思う。
すぐに思い浮かぶのが、下の図。
1569年、フランドル(現ベルギー)出身の地理学者ゲラルドゥス・メルカトルが考案した地図投影法です。
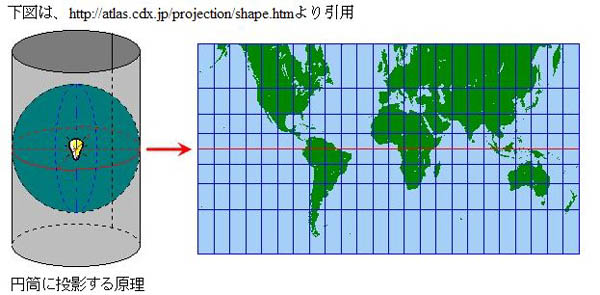
メルカトル図法って、小学校の高学年ぐらいで習っただろうか・・・
いや、中学だったかな?
原理が簡単でイメージしやすいので、「あ、そーか」くらいにしか思っていなかった。
おまけに、こんな事考えたくらいで、何で名前が付くの?・・とも思っていた。
しかしこの図法、実はちょっとした隠し味が仕込んであったのだ。
隠し味だから、何十年もそれに気付かずに地図を使っていた。
メルカトルさんって、本当、頭がいいなぁ~ ・・と改めて関心した。
---------------------------------
さて、何に関心したかを説明いたそう。
普段、私達が使っている地図って、東西方向も南北方向も同じ縮尺で出来てますよね。
地図にコンパスで円を描けば、円の中心からの距離は、
どこも同じになるように出来てます。
あまりに当たり前なので、どうしてそうなっているか、考えた事もありませんでした。
でも、小学校で習ったメルカトル図法の原理を、ちゃんと検証してみると、
東西と南北の投影倍率が異なってしまうんですよ~。
何を言っているかというと、
例えば地球上のある地点Aでの、東西1kmの線分と南北1kmの線分をそれぞれ
メルカトル図法の円筒面に投影したときの投影倍率を計算すると、同じにならないんです。
しかも、その倍率差が一定ではなく、緯度が高くなるほど大きくなるんです。
これじゃ、地図として使えません。
距離だけじゃなく、角度も実際と違ってしまいます。

具体的に、どの程度ちがうのかエクセルで計算してみました。 →図3
この結果、例えば北緯37度では、南北方向が東西方向より25%も大きく投影される事が
わかったのです。

たぶん、メルカトルさんも悩んだことでしょう。
当時、海を航海する上では角度がとても重要で、
角度が実際と異なるような地図は使い物にならなかったはずです。
(このあたりは、今も昔も同じだとは思いますが・・)
そこで、メルカトルさんは、ちょっとした隠し味を含ませたのです。
ちゃんと説明しようとすると、複雑な数式が出てきます。
ボケてきた私には説明できないので、結果だけ示します。 →図4、5
そうなんです。
メルカトルさんは、東西方向と南北方向の投影倍率が同じになるように、
こっそり補正を加えていたんです。
いや~、これじゃ気が付かないはずだよ。

普段、当たり前に使っていた地図に、こんな隠し味が入っていたとは知りませんでした。
メルカトルさんのお陰で、いつも便利に使わせてもらってたんですね。
メルカトルさん、ありがとう!
ひょんな事から、メルカトル図法に大きな興味を持った。
”メルカトル図法”と言えば、誰でも一度は聞いたことはあると思う。
すぐに思い浮かぶのが、下の図。
1569年、フランドル(現ベルギー)出身の地理学者ゲラルドゥス・メルカトルが考案した地図投影法です。

メルカトル図法って、小学校の高学年ぐらいで習っただろうか・・・
いや、中学だったかな?
原理が簡単でイメージしやすいので、「あ、そーか」くらいにしか思っていなかった。
おまけに、こんな事考えたくらいで、何で名前が付くの?・・とも思っていた。
しかしこの図法、実はちょっとした隠し味が仕込んであったのだ。
隠し味だから、何十年もそれに気付かずに地図を使っていた。
メルカトルさんって、本当、頭がいいなぁ~ ・・と改めて関心した。
---------------------------------
さて、何に関心したかを説明いたそう。
普段、私達が使っている地図って、東西方向も南北方向も同じ縮尺で出来てますよね。
地図にコンパスで円を描けば、円の中心からの距離は、
どこも同じになるように出来てます。
あまりに当たり前なので、どうしてそうなっているか、考えた事もありませんでした。
でも、小学校で習ったメルカトル図法の原理を、ちゃんと検証してみると、
東西と南北の投影倍率が異なってしまうんですよ~。
何を言っているかというと、
例えば地球上のある地点Aでの、東西1kmの線分と南北1kmの線分をそれぞれ
メルカトル図法の円筒面に投影したときの投影倍率を計算すると、同じにならないんです。
しかも、その倍率差が一定ではなく、緯度が高くなるほど大きくなるんです。
これじゃ、地図として使えません。
距離だけじゃなく、角度も実際と違ってしまいます。

具体的に、どの程度ちがうのかエクセルで計算してみました。 →図3
この結果、例えば北緯37度では、南北方向が東西方向より25%も大きく投影される事が
わかったのです。

たぶん、メルカトルさんも悩んだことでしょう。
当時、海を航海する上では角度がとても重要で、
角度が実際と異なるような地図は使い物にならなかったはずです。
(このあたりは、今も昔も同じだとは思いますが・・)
そこで、メルカトルさんは、ちょっとした隠し味を含ませたのです。
ちゃんと説明しようとすると、複雑な数式が出てきます。
ボケてきた私には説明できないので、結果だけ示します。 →図4、5
そうなんです。
メルカトルさんは、東西方向と南北方向の投影倍率が同じになるように、
こっそり補正を加えていたんです。
いや~、これじゃ気が付かないはずだよ。

普段、当たり前に使っていた地図に、こんな隠し味が入っていたとは知りませんでした。
メルカトルさんのお陰で、いつも便利に使わせてもらってたんですね。
メルカトルさん、ありがとう!



















