「または」…∪、「かつ」…∩です。例えば、Aさんは、「野球もサッカーも、両方とも得意である訳ではない」とは、どういうことでしょうか。それは、「野球が得意ではないか、サッカーが得意ではない。(野球もサッカーも得意ではないというのも含む)」ということですね。これを図にすると、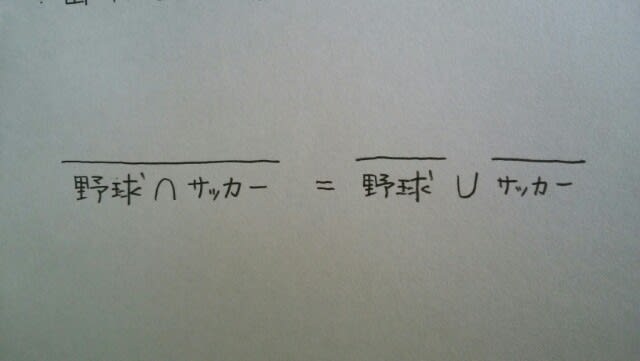 ポイントはここです。
ポイントはここです。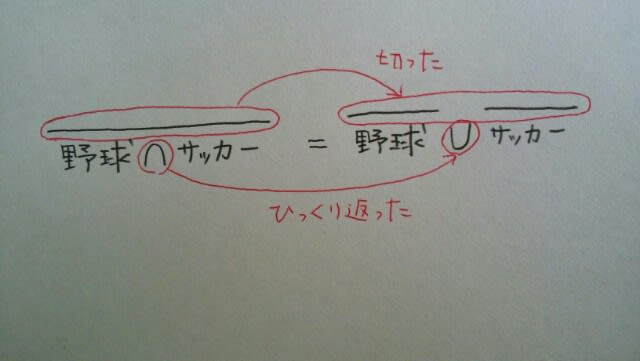 「野球かサッカーが得意だということではない」とは、どういうことでしょうか?それは、「野球もサッカーも得意ではない」です。
「野球かサッカーが得意だということではない」とは、どういうことでしょうか?それは、「野球もサッカーも得意ではない」です。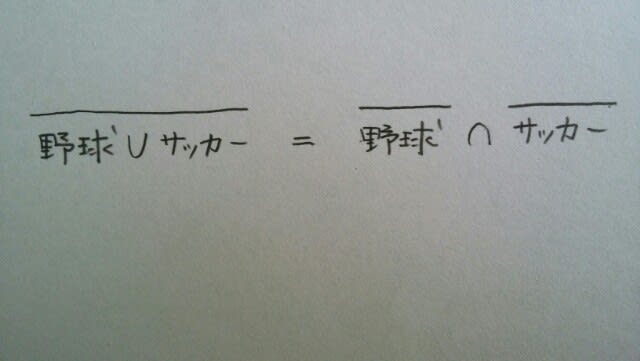 やはり、
やはり、 どちらも、長い横棒を切ると、∩や∪がひっくり返りますね。これを、ド・モルガンの法則といいます。 次は、警視庁(大卒)の過去問です。 ある事件の犯人について、「彼が車を運転できて、かつ、左利きでなければ、彼はそのめがねの持ち主である。」という命題が成り立つときに論理的に必ず成り立つ命題として、最も妥当なのはどれか。 ①彼が車の運転をできず、かつ、左利きであるならば、彼はそのめがねの持ち主である。 ②彼が車の運転をできないか、または、左利きであるならば、彼はそのめがねの持ち主ではない。 ③彼が車の運転をできず、かつ、そのめがねの持ち主であるならば、彼は左利きである。 ④彼がそのめがねの持ち主であるならば、彼は車を運転できて、かつ、左利きではない。
どちらも、長い横棒を切ると、∩や∪がひっくり返りますね。これを、ド・モルガンの法則といいます。 次は、警視庁(大卒)の過去問です。 ある事件の犯人について、「彼が車を運転できて、かつ、左利きでなければ、彼はそのめがねの持ち主である。」という命題が成り立つときに論理的に必ず成り立つ命題として、最も妥当なのはどれか。 ①彼が車の運転をできず、かつ、左利きであるならば、彼はそのめがねの持ち主である。 ②彼が車の運転をできないか、または、左利きであるならば、彼はそのめがねの持ち主ではない。 ③彼が車の運転をできず、かつ、そのめがねの持ち主であるならば、彼は左利きである。 ④彼がそのめがねの持ち主であるならば、彼は車を運転できて、かつ、左利きではない。
⑤彼がそのめがねの持ち主でないならば、彼は車を運転できないか、または、左利きである。 対偶は、
対偶は、 これの、矢印の右側を、ドモルガンの法則で書き換えると、
これの、矢印の右側を、ドモルガンの法則で書き換えると、 これは、肢⑤のことです。
これは、肢⑤のことです。
 < />にほんブログ村
< />にほんブログ村
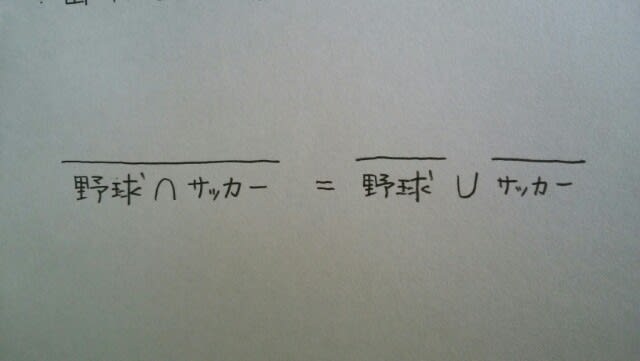 ポイントはここです。
ポイントはここです。 「野球かサッカーが得意だということではない」とは、どういうことでしょうか?それは、「野球もサッカーも得意ではない」です。
「野球かサッカーが得意だということではない」とは、どういうことでしょうか?それは、「野球もサッカーも得意ではない」です。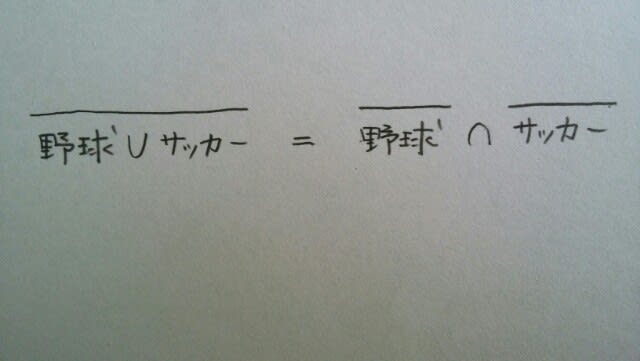 やはり、
やはり、 どちらも、長い横棒を切ると、∩や∪がひっくり返りますね。これを、ド・モルガンの法則といいます。 次は、警視庁(大卒)の過去問です。 ある事件の犯人について、「彼が車を運転できて、かつ、左利きでなければ、彼はそのめがねの持ち主である。」という命題が成り立つときに論理的に必ず成り立つ命題として、最も妥当なのはどれか。 ①彼が車の運転をできず、かつ、左利きであるならば、彼はそのめがねの持ち主である。 ②彼が車の運転をできないか、または、左利きであるならば、彼はそのめがねの持ち主ではない。 ③彼が車の運転をできず、かつ、そのめがねの持ち主であるならば、彼は左利きである。 ④彼がそのめがねの持ち主であるならば、彼は車を運転できて、かつ、左利きではない。
どちらも、長い横棒を切ると、∩や∪がひっくり返りますね。これを、ド・モルガンの法則といいます。 次は、警視庁(大卒)の過去問です。 ある事件の犯人について、「彼が車を運転できて、かつ、左利きでなければ、彼はそのめがねの持ち主である。」という命題が成り立つときに論理的に必ず成り立つ命題として、最も妥当なのはどれか。 ①彼が車の運転をできず、かつ、左利きであるならば、彼はそのめがねの持ち主である。 ②彼が車の運転をできないか、または、左利きであるならば、彼はそのめがねの持ち主ではない。 ③彼が車の運転をできず、かつ、そのめがねの持ち主であるならば、彼は左利きである。 ④彼がそのめがねの持ち主であるならば、彼は車を運転できて、かつ、左利きではない。 ⑤彼がそのめがねの持ち主でないならば、彼は車を運転できないか、または、左利きである。
 対偶は、
対偶は、 これの、矢印の右側を、ドモルガンの法則で書き換えると、
これの、矢印の右側を、ドモルガンの法則で書き換えると、 これは、肢⑤のことです。
これは、肢⑤のことです。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます