抽象的に考えるほうが良いとき

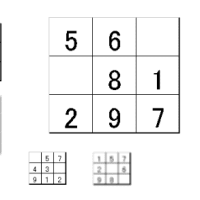
　「３×５の升目にはいくつの四角形が含まれているか」という問題を考えるとき、たいていの人はＡのような図を描いて考えると思います。
　Ｂのように縦長の図を描いても良いのですが、横長に描くほうが自然に感じられます。
　全体をとらえるのには横長に見るほうが自然で、縦長に見るほうがとらえにくいのです。
　同じように５×３×３の直方体を描く場合でも、Ｄ図のようには描かずＥ図のように横長に描くのが自然です。

　ところで、実際にこの問題の答えを出そうとするにはどのように考えるでしょうか。
　たいていの人は一番小さな升目をまずかぞえ、次に小さな升目が二つ合わさったもの、次に三つ合わさったものと順にかぞえていって合計を出そうとします。
　答えは９０個ですから、かぞえ方をきちんと組織立ててやらないと、かぞえ間違いが起きてしまいます。
　たとえば２個合わさったものは、縦１×横２のものと、縦２×横１のものがありますが、
４個合わさったものは縦１×横４の場合と、縦２×横２の場合です。
　また５個合わさったものは縦１×横５だけですが、６個合わさったものは、縦２×横３の場合と、縦３×横２の場合があります。

　こうしたかぞえ方は、そのつど具体的にかぞえていくので、升目が増えるとたくさんの計算をしなければならないので、能率が悪く見落としも出てきます。
　たとえば１０×１５などとなってくればとても大変です。
　年をとると具体的な考え方に執着しがちで、抽象的な考え方が苦手になるといいますが、具体的な考え方だけではうまくいかない場合もあるのです。

　この問題の場合、四角形は二本の縦線と二本の横線で囲まれたものですから、日本の縦線を選ぶ選び方を数え、それに対して二本の横線の選び方を数え、この二つをかければよいのです。
　Ａ図では縦線は６本、横線は４本です。
　縦線の最初の一本の選び方は６通りで、それぞれに対してもう一本の選び方は５通りですから、全部で６×５で３０通りですが、同じ線が１本目にも、２本目にも選ばれているので実際の選び方は３０÷２で１５通りとなります。
　同じように計算すると横の２本の線の選び方は４×３÷２で６通りです。
　そこで四角形の数は１５×６で９０個となります。

　これを応用すればＥ図に含まれている直方体の数は１５×６×６で５４０個となりますが、これを具体的な方法で数え上げるというのはとてもできたものではありません。
　数が多いというだけでなく、立体図では見えないところができてしまうので、具体的に眼で見て数え上げるということができなくなるからです。