視覚能力があるほうが錯視するとき

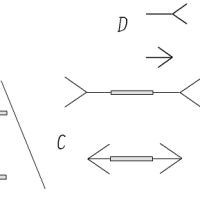
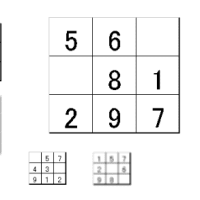
　左上の図形はザンダーの平行四辺形という錯視図形で、線ａとｂは同じ長さなのですが、ａのほうが長く見えます。
　なぜａのほうが長く見えるかという説明で、心理学のテキストでは矢羽根の錯視によるとしているようです。
　矢羽根が広がっているほうが軸線が長く見えるというのですが、実際左下の例で見ると、上の矢羽根のほうが長いかといえばそんなことはありません。
　同じかむしろ、下のほうがややもすると長く見えるのですから、この説明は間違いです。
　もう少しまともな理由を考えて見ます。
　
　左下に三角形がありますが、辺ｘとｙとを比べればｙのほうが長いことがすぐ分かります。
　このときｘに対する角ｄとｙに対する角ｄを比べれば明らかにｃのほうがｄより大きいです。
　つまり三角形では大きい角に対する辺のほうが小さい角に対する辺より長いのですが、これは中学の数学の知識の範囲です。
　次に右の図の角ｅと角ｆを比べるとどちらが大きく見えるかといえば、ｆのほうが大きく見えるでしょう。
　ｅとｆは同じ大きさの角なのですが、隣接する角との対比でｅは小さく見え、ｆは大きく見えるのです。
　そうすると三角形ＡＢＣでは角Ｂより角Ｃのほうが大きく見えるので辺ＡＢのほうが辺ＡＣより長く見える、つまりａのほうがｂより長く見えます。

　辺ＡＢが辺ＡＣより長く見えるということは角Ｃのほうが角Ｂより大きく見えるということだというのは中学数学の知識で分かることです。
　それならなぜ角Ｃのほうが角Ｂより大きく見えるかを考えればよいのです。
　矢羽根の錯視を説明に持ってくるのはいかにも心理学的な説明で、形の類似からの類推で、直接的な説明ではありません。

　ところで、この錯視図を見て誰でもがａのほうがｂより長く見えるかといえば、そうとは限りません。
　線ａと線ｂしか見なければａのほうが特段長く見えるということはないかもしれません。
　三角形ＡＢＣを意識すれば、無意識のうちに角Ｂと角Ｃを比較してしまうので、辺ＡＢのほうが長く見えてしまうのです。
　つまり視野を広くして見る、すなわち視覚能力があるほうが錯視が発生するのです。
　そうしたことを知った上で、辺ＡＣに注意を集中して見ると、角度に注意が向けられないため、辺ＡＢと辺ＡＣは同じ長さに見えるようになります。