２０２０年日本ジュニア数学オリンピック予選の問題（６）

こんにちは。東久留米市の学習塾塾長です。

今回は、２０２０年日本ジュニア数学オリンピック予選の問題です。

問題は、
「一辺の長さが５の立方体の８つの隅から一辺の長さが１の立方体を取り除いた図形Ｑを考える。また一辺の長さが１の立方体４個からなる図のようなブロックＬと一辺の長さが１の立方体がいくつかある。

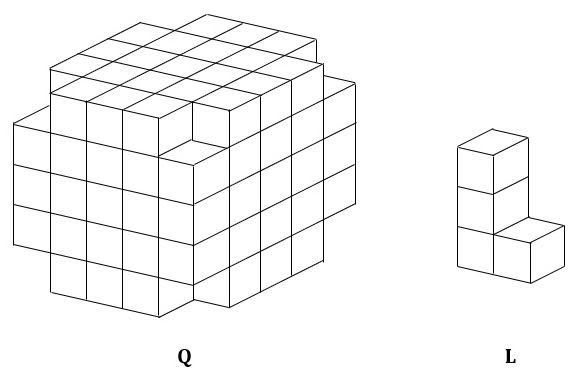
Ｌと一辺の長さが１の立方体いくつかを貼りあわせてＱを作るとき、用いるＬの個数としてありうる最大の値を求めよ。」
です。

早速、取り掛かりましょう。

平面上のマス目を市松模様に塗り分けるように、Ｑを市松模様ぽく、つまり、一辺の長さが１の２つの立方体で面を共有するもの同士は異なる色になるように塗り分けます。

ここでは、Ｑを５層の立体と考え、下側から１、２、…、５層として、それぞれの層を図１のように白黒に塗り分けました。

▲図１．Ｑを塗り分けました

Ｑは一辺の長さが１の立方体（以下、立方体）
５×５×５－８＝１１７（個）
からなり、ここでＱを構成するＬの個数をｌ個、Ｑを構成する一辺の長さが１の立方体（以下、Ｓ）の個数をｓ個とすると、
４ｌ＋ｓ＝１１７　　　（１）
が成り立ちます。

次に黒で塗った立方体の個数に注目します。

図１に示した塗り分けで、黒で塗られた立方体の個数は、
１２＋１３＋１２＋１３＋１２＝６２（個）
で、このとき、ＬがＱのいずれの位置におかれても必ず黒で塗った立方体を２個含み、一方、Ｓは高々１個の黒く塗られた立方体を含むので、
２ｌ＋ｓ≧６２　　　　（２）
が成り立ちます。

すると、（１）と（２）から
２ｌ＋１１７－４≧６２
２ｌ≦５５
ｌ≦２７．５
で、ｌは整数なので、
ｌ≦２７
です。

したがって、Ｌの個数は多くても２７個ということが判りました。

それではここから、２７個のＬと９個（１１７－４×２７＝９）のＳを貼りあわせてＱを作ることができるかどうかを調べましょう。

そこで図２の左側の図のように、１と５層のそれぞれに、高さが１になるように４個のＬを置き、右側の図のように、２、３、４層のそれぞれに、高さが１になるように６個のＬを置きました。

▲図２．１、５層にＬを４個、２，３，４層にＬを６個置きました

すると、１から５層まで合わせて、４×２＋６×３＝２６（個）のＬを置くことができることが判りました。

あとは、もう一つＬを置くことができるかということですが、それは可能で、例えば図３に示した１、２、３層目の赤色でマークした部分に１個のＬを置くことができます。このとき、Ｌの高さは３になります。

▲図３．１、２、３層の赤色でマークした部分にＬを１個置くことができます

したがって、図４のようにLを配置することにより、２６＋１＝２７（個）のLを置くことができることが判りました。ここで、黄色でマークした部分がＳになります。

以上から、Ｑを作るとき、用いるＬの個数としてありうる最大の値は ２７ で、これが答えです。


簡単な問題です。