こんにちは。東久留米市の学習塾塾長です。
今回は、組合せ問題です。
問題は、
「10以下の正の整数から、いずれの2つの差も2以上であるような3個の整数を選ぶ方法は何通りか。ただし、順番を変えただけの選び方は同じものとして数える。」
です。
問題の条件をみたすような3個の正整数を小さい順に a1、a2、a3 とすると、
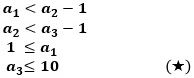
が成り立ちます。
このとき、
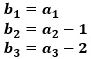
とすると、(★)は、
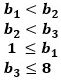
になります。
これは、1以上8以下の整数を3個選び、それらの小さい順に0、1、2を加えた3個の整数は、問題の条件をみたすことを示します。
したがって、問題の条件を満たす3個の整数の選び方は、
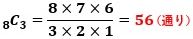
で、これが答えです。
簡単な問題です。
今回は、組合せ問題です。
問題は、
「10以下の正の整数から、いずれの2つの差も2以上であるような3個の整数を選ぶ方法は何通りか。ただし、順番を変えただけの選び方は同じものとして数える。」
です。
問題の条件をみたすような3個の正整数を小さい順に a1、a2、a3 とすると、
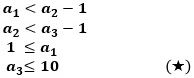
が成り立ちます。
このとき、
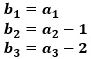
とすると、(★)は、
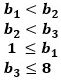
になります。
これは、1以上8以下の整数を3個選び、それらの小さい順に0、1、2を加えた3個の整数は、問題の条件をみたすことを示します。
したがって、問題の条件を満たす3個の整数の選び方は、
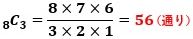
で、これが答えです。
簡単な問題です。










