こんにちは。東久留米市の学習塾塾長です。
今回は、平成27年度東大大学院理学系研究科地球惑星科学専攻の入試問題です。
問題は、
「

のとき、u+2v+4wの最大値を求めよ。ただし、u、v、wは実数とする。」
です。
u=U、2v=V、4w=Wとすると、

のとき、U+V+Wの最大値を求めることになります。
このとき、
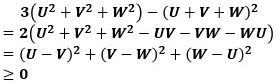
から

が成り立ちます。
これに(★)を代入すると、

になり、これから

です。
したがって、
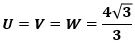
つまり、

のとき、u+2v+4wは

になり、これが答えです。
2次式を球、1次式を平面として球に接する平面を調べてもOKです。
今回は、平成27年度東大大学院理学系研究科地球惑星科学専攻の入試問題です。
問題は、
「

のとき、u+2v+4wの最大値を求めよ。ただし、u、v、wは実数とする。」
です。
u=U、2v=V、4w=Wとすると、

のとき、U+V+Wの最大値を求めることになります。
このとき、
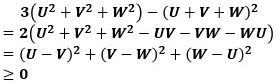
から

が成り立ちます。
これに(★)を代入すると、

になり、これから

です。
したがって、
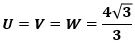
つまり、

のとき、u+2v+4wは

になり、これが答えです。
2次式を球、1次式を平面として球に接する平面を調べてもOKです。










