こんにちは。東久留米市の学習塾塾長です。
今回は、平成10年度東大大学院理学系研究科物理学専攻の入試問題の続きです。
問題は、
「A、Bの2人があるゲームを繰り返し行う。Aが2回続けて勝つまでゲームを続ける。各々のゲームでAが勝つ確率は2/3とする。
(a) N回のゲームでも終了しない確率を
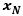
とする。
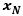
を
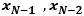
で表せ。
(b)
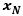
をNの関数として求めよ。
(c) 行なわれるゲームの回数の期待値を求めよ。」
で、今回は(b)です。
前回求めた(a)の答えの3項間漸化式
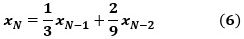
の特性方程式

の解は、
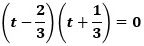
から
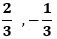
なので、
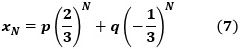
とすると、これは(6)を満たします。(計算は省略します)
ここで(7)の係数p、qを求めるために

の値を計算します。
・ N=2のときにゲームが終了しない

は、Aの勝ちと負け(引き分けを含む)をそれぞれ○および×とした場合、○×、×○、××なので、
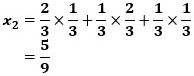
です。
・ N=3のときにゲームが終了しない
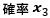
は、○×○、○××、×○×、××○、×××なので、

です。
これらと(7)から

が成り立ち、この連立方程式を解くと、

です。
これらを(7)に代入して整理すると、

で、これが(b)の答えです。
(c)は次回です。
今回は、平成10年度東大大学院理学系研究科物理学専攻の入試問題の続きです。
問題は、
「A、Bの2人があるゲームを繰り返し行う。Aが2回続けて勝つまでゲームを続ける。各々のゲームでAが勝つ確率は2/3とする。
(a) N回のゲームでも終了しない確率を
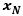
とする。
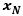
を
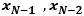
で表せ。
(b)
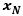
をNの関数として求めよ。
(c) 行なわれるゲームの回数の期待値を求めよ。」
で、今回は(b)です。
前回求めた(a)の答えの3項間漸化式
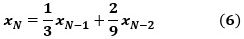
の特性方程式

の解は、
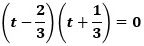
から
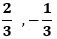
なので、
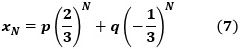
とすると、これは(6)を満たします。(計算は省略します)
ここで(7)の係数p、qを求めるために

の値を計算します。
・ N=2のときにゲームが終了しない

は、Aの勝ちと負け(引き分けを含む)をそれぞれ○および×とした場合、○×、×○、××なので、
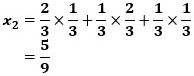
です。
・ N=3のときにゲームが終了しない
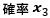
は、○×○、○××、×○×、××○、×××なので、

です。
これらと(7)から

が成り立ち、この連立方程式を解くと、

です。
これらを(7)に代入して整理すると、

で、これが(b)の答えです。
(c)は次回です。










