見えたとおりに描いて失敗

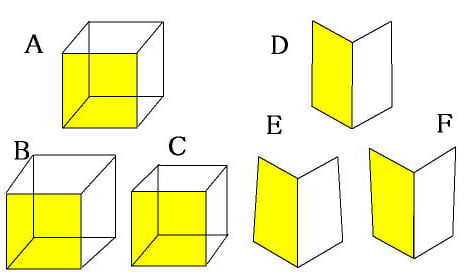
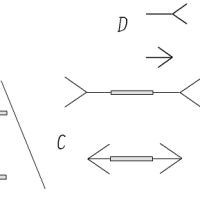
　図Ａは立方体に見えますが、黄色い正方形の面が前方にせり出して見えたり、あるいは広報に後退して見えたりします。
　反対側にあるもうひとつの正方形は黄色い正方形と同じ大きさなのですが、、黄色い面が前方に見えるときは、黄色い面のほうが小さく見えます。
　逆に黄色い面が後退して見えるときは黄色い面のほうが大きく見えます。
　図が立方体に見えるため、奥行き感が生じ、前方にせり出して見えるときは焦点が変化して、小さく見えるのです。

　もし黄色い面が小さく見えた状態を記憶して、図を模写するとすればＣのような図を描くことになりますし、逆に大きく見えたときの記憶で模写すればＢのような図を描くことになります。
　いずれもＡが立方体であると思って模写するのですが、見え方が変化するため違った図を描くことになります。
　見えたとおりに描こうとしても、見え方が変化するので、見えたとおりに描こうとすると見本と違った結果になるのです。
　
　模写を成功させようとするなら、右脳を使って見えたとおりに模写をすべきだという説がありますが、この場合は逆になります。
　左脳を使うなら、立方体を見たとき前方に見える面は後方の面より大きく見えるはずですから、黄色い面が前方にあると思えば黄色い面のほうを大きく描くはずです。
　ところが黄色い面が前方にあると思ったときは、黄色い面のほうが小さく見えているので、見えたとおり小さく描けば元の図とは違ってしまうのです。

　同じように、Ｄ図の場合も上が広がって見えたり、狭まって見えたりするので、見えたとおりに模写をしようとすると元の図と違ったものになってしまいます。
　間違いのもとは、平面図形なのに奥行きを感じて、三次元のものを見るように焦点を動かして見てしまうからです。
　人間の目はもともと三次元のものを見るようにできていて、平面に三次元像を写すことは不得意です。
　三次元の世界でものを見るときは、見るものの距離に応じて焦点距離を変えて見ています。
　平面を見るときにも焦点距離を変えてしまえば、実際とは違った見え方になってしまいます。
　
　平面に三次元の像を写そうとするなら、写真のように焦点を動かさないで見た状態で写すべきです。
　ところが焦点を動かさず、視線を動かさずに見た場合は焦点の当てられている部分しかハッキリ見えません。
　どうしても目を動かさなければならないので、遠近法とかいろんな技法を使ってつまり左脳に頼って描くということになります。
　絵を描いたりするのは右脳のはたらきだと思い込んでいても、実際は左脳にも大きく依存しているのです。