
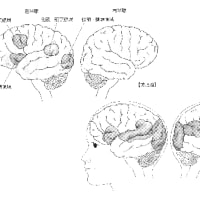
図Aの上の二つの図形のうち、左側は円柱が倒れて前を向いているように見え、右側は上に向かって立っているように見えます。
円が重なって描かれているため奥行きが感じられるためにそのように見えるのですが、その結果二つの図形は直角を作っているように見えます。
その下の図は上の図を囲む長方形を書き加えたものですが、その結果上の図では感じられた奥行き感がほとんどなくなっています。
周りを囲む長方形があるため、長方形に囲まれた部分が平面的に見え、その結果奥行きを感じなくなっています。
長方形をひとつの平面としてみるため、焦点距離を動かさないで見ることになり、奥行き感が発生しないのです。
つまり、上の図を見るときは気がつかないうちに視線を動かし、焦点距離を変えながら見ているということになります。
したがって、上の図を見るときでも視線を動かさずに、焦点距離を変えないで凝視すれば奥行き感は発生しないはずです。
事実、上の二つの図の真ん中あたりに視線を向け、視線を動かさずにじっと見続けると、二つの図形は奥行き感がなくなり同じ平面上にあるように見えます。
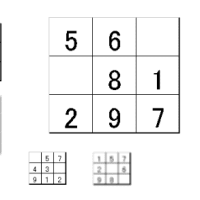
B図の場合は何気なしに見れば、二本の円柱が直交しているように見えます。
左の円柱は右上に向かって伸びているように見え、右の円柱は右後方に向かって横たわっているように見えます。
どちらの円柱も奥行き感があるため、目に近く感じる側が細く、反対側が太く見えます。
左の図の一番上の円と、右の図の一番下の円は距離が離れているように感じますが、図上での位置はすぐ近くです。
ここで図に描かれている長方形に注意を向けると、左の円と右の半分隠された円とが同じ平面のすぐ近くの円に見えます。
そうすると奥行き感がなくなり、二つの円柱は平行に見え、両端の太さは同じに見えるようになります。
視線を動かさず、焦点距離を変えなければ見え方が変らないからです。
C図も同じ現象で、一番上の円柱は左が手前に見え、右が奥に見えるので右側が太くなっているように見えます。
これを左右反転したのが真ん中の図で右側が手前に見え、左側が奥に見えますから上の円柱とは交差して見えます。
一番下の図は上の図に長方形を書き加えたものですが、この長方形に注意を向けると、長方形の平面性に注意が向けられるため、円柱の奥行き感がなくなり、平たく見えるようになります。
普通に絵や図を見るときは、目を動かしながらいろいろな部分を見ているので、見る部分によって焦点が変化したりします。
カメラのように焦点を固定し、レンズを動かさないで見るわけではないので、人間が見たと思っている像は、一つの網膜像ではなく、いくつかの網膜像の複合なのです。
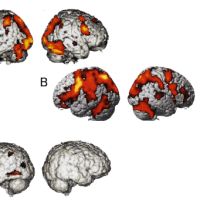
絵や写真を見たときの目の注視点の動きを示した図というのを見ると、絵をジッと同じ点に向けてみているのでなく、あちこちに視点を飛ばして見ていることが分ります。
カメラがこのような動きをしながら写していれば、映像が流れてしまってまとまりがつきません。
もしものをありのままに見ようとするなら、カメラのように目を動かさず、
焦点距離も動かさずに見るということになりますが、そうするとすべてが平板に見えてしまいかえって不便になるのです。
。













※コメント投稿者のブログIDはブログ作成者のみに通知されます