こんにちは。東久留米市の学習塾塾長です。
空模様は花曇りといった感じですが、気温は昨日より高く暖かい日になりました。桜もそろそろお仕舞いの頃に近づいたようです。
さて、今回は平成23年度京大入試問題(前期、文系)です。
問題は、
「[1]辺AB、辺BC、辺CAの長さがそれぞれ12、11、10の三角形ABCを考える。
∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
[2]箱の中に、1から9までの番号を1つずつ書いた9枚のカードが入っている。ただし、異なるカードには異なる番号が書かれているものとする。この箱から2枚のカードを同時に選び、小さい方の数をXとする。これらのカードを箱に戻して、再び2枚のカードを同時に選び、小さい方の数をYとする。X=Yである確率を求めよ。」
です。
一つの大問のなかに、図形と確率の小問が一つずつあって、何か中学や高校の入試問題のようですね。
まず、[1]から片付けましょう。
初めに問題の図を描きます。(図1)

▲図1.問題の図を描きました
三角形の3辺の長さが決まっていると、その三角形のすべての要素、例えば、面積や角の大きさなど、は、すべて決まります。つまり、この問題のような一つの頂点と対辺の中点を結んだ線分の長さも決まっていて、計算で求めることができます。
そこで、角の二等分線定理を利用すると、
BD:DC=AB:AC=12:10=6:5
なので、図2のように、
BD=6
DC=5
になります。(線分ADの長さをxとしました)

▲図2.角の二等分線定理からBD=6、DC=5です
ここで、高校で勉強する三角関数の余弦定理を使うと簡単ですが、まず、それを使わずに解きましょう。
まず図3のように、頂点Aから辺BCに垂線を下ろし、その足をHとし、線分AH、線分CHの長さをそれぞれh、yとします。
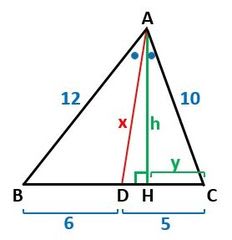
▲図3.頂点Aから辺BCに垂線を下ろしました
ここで、△ABHと△ACHに三平方の定理を適用すると、
AB^2=BH^2+AH^2
から
144=(11-y)^2+h^2 (1)
が成り立ち、さらに、
AC^2=CH^2+AH^2
から
100=y^2+h^2 (2)
が成り立ちます。
そこで、(1)-(2)から
44=(11-y)^2-y^2
=121-22y+y^2-y^2
=121-22y
22y=77
y=7/2
です。
これを(2)に代入して、
100=49/4+h^2
から
h^2=351/4
です。
最後に、△ADHに三平方の定理を適用して、
AD^2=DH^2+AH^2
x^2=(5-y)^2+h^2
=(5-7/2)^2+351/4
=9/4+351/4
=360/4
=90
で、x>0から
x=3√10
で、これが答えです。
次に三角関数を利用して解いてみましょう。
まず、△ABDに余弦定理を適用すると、
cos●=(AB^2+AD^2-BD^2)/(2AB・AD)
=(144+x^2-36)/(2・12x)
=(108+x^2)/(24x)
で、さらに△ACDに余弦定理を適用して、
cos●=(AC^2+AD^2-DC^2)/(2AC/AD)
=(100+x^2-25)/(2・10x)
=(75+x^2)/(20x)
になります。
これらから、
(108-x^2)/(24x)=(75+x^2)/(20x)
が成り立つので、これを整理して、
x^2=90
から
x=±3√10
で、
x>0なので、
x=3√10
と、先ほどの答えと一致しました。
続いて、[2]です。問題を再掲します。
「[2]箱の中に、1から9までの番号を1つずつ書いた9枚のカードが入っている。ただし、異なるカードには異なる番号が書かれているものとする。この箱から2枚のカードを同時に選び、小さい方の数をXとする。これらのカードを箱に戻して、再び2枚のカードを同時に選び、小さい方の数をYとする。X=Yである確率を求めよ。」
まず、下のような表を作りましょう。
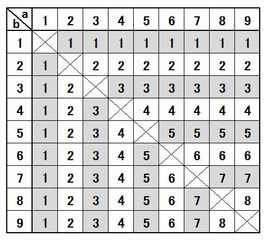
▲表.2枚のカードに書かれている数とX(Y)をまとめました
この表は、選んだ2枚のカードに書かれている数aとbと、XまたはYの関係を表しています。
例えば、a=4、b=6を選んだとすると、そのうちの小さい方がXまたはYになるので、X(Y)=4になります。
そこで、この表からX(Y)がn(n=1,2,3・・・,9)になる確率を求めましょう。
9枚のカードから2枚を選ぶ場合の数は、
9×8=72(通り)
です。
一方、n=1,2,3,・・・、9になる場合の数は、表から、それぞれ、
n=1 16(通り)
n=2 14(通り)
n=3 12(通り)
n=4 10(通り)
n=5 8(通り)
n=6 6(通り)
n=7 4(通り)
n=8 2(通り)
n=9 0(通り)
です。
したがって、n=1,2,3,・・・,9になる確率は、それぞれ、
n=1 16/72
n=2 14/72
n=3 12/72
n=4 10/72
n=5 8/72
n=6 6/72
n=7 4/72
n=8 2/72
n=9 0/72
になります。
そして、X=Yとなるのは、XもYも同じnになるということなので、その確率Pは、
P=(16/72)^2+(14/72)^2+(12/72)^2+(10/72)^2+(8/72)^2+(6/72)^2+(4/72)^2+(2/72)^2+(0/72)^2
=(8/36)^2+(7/36)^2+(6/36)^2+(5/36)^2+(4/36)^2+(3/36)^2+(2/36)^2+(1/36)^2
=(64+49+36+25+16+9+4+1)/36^2
=204/36^2
=17/108
で、これが答えです。(2乗和の公式を使えば簡単に計算できます)
また、表を作らないのであれば、X(Y)=1,2,3,・・・,9になる確率を次のように計算できます。
つまり、X(Y)=1になる確率p(1)は、2枚のカードのうち1枚が1で、もう1枚が2,3,4,・・・、9のときなので、
p(1)=1/9×8/8×2=16/72
で、同様に、
p(2)=1/9×7/8×2=14/72
p(3)=1/9×6/8×2=12/72
・・・・・
p(9)=1/9×0/8×2= 0/72
となり、先ほどの途中結果と同じになります。
どちらも簡単な問題でした。
空模様は花曇りといった感じですが、気温は昨日より高く暖かい日になりました。桜もそろそろお仕舞いの頃に近づいたようです。
さて、今回は平成23年度京大入試問題(前期、文系)です。
問題は、
「[1]辺AB、辺BC、辺CAの長さがそれぞれ12、11、10の三角形ABCを考える。
∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
[2]箱の中に、1から9までの番号を1つずつ書いた9枚のカードが入っている。ただし、異なるカードには異なる番号が書かれているものとする。この箱から2枚のカードを同時に選び、小さい方の数をXとする。これらのカードを箱に戻して、再び2枚のカードを同時に選び、小さい方の数をYとする。X=Yである確率を求めよ。」
です。
一つの大問のなかに、図形と確率の小問が一つずつあって、何か中学や高校の入試問題のようですね。
まず、[1]から片付けましょう。
初めに問題の図を描きます。(図1)

▲図1.問題の図を描きました
三角形の3辺の長さが決まっていると、その三角形のすべての要素、例えば、面積や角の大きさなど、は、すべて決まります。つまり、この問題のような一つの頂点と対辺の中点を結んだ線分の長さも決まっていて、計算で求めることができます。
そこで、角の二等分線定理を利用すると、
BD:DC=AB:AC=12:10=6:5
なので、図2のように、
BD=6
DC=5
になります。(線分ADの長さをxとしました)

▲図2.角の二等分線定理からBD=6、DC=5です
ここで、高校で勉強する三角関数の余弦定理を使うと簡単ですが、まず、それを使わずに解きましょう。
まず図3のように、頂点Aから辺BCに垂線を下ろし、その足をHとし、線分AH、線分CHの長さをそれぞれh、yとします。

▲図3.頂点Aから辺BCに垂線を下ろしました
ここで、△ABHと△ACHに三平方の定理を適用すると、
AB^2=BH^2+AH^2
から
144=(11-y)^2+h^2 (1)
が成り立ち、さらに、
AC^2=CH^2+AH^2
から
100=y^2+h^2 (2)
が成り立ちます。
そこで、(1)-(2)から
44=(11-y)^2-y^2
=121-22y+y^2-y^2
=121-22y
22y=77
y=7/2
です。
これを(2)に代入して、
100=49/4+h^2
から
h^2=351/4
です。
最後に、△ADHに三平方の定理を適用して、
AD^2=DH^2+AH^2
x^2=(5-y)^2+h^2
=(5-7/2)^2+351/4
=9/4+351/4
=360/4
=90
で、x>0から
x=3√10
で、これが答えです。
次に三角関数を利用して解いてみましょう。
まず、△ABDに余弦定理を適用すると、
cos●=(AB^2+AD^2-BD^2)/(2AB・AD)
=(144+x^2-36)/(2・12x)
=(108+x^2)/(24x)
で、さらに△ACDに余弦定理を適用して、
cos●=(AC^2+AD^2-DC^2)/(2AC/AD)
=(100+x^2-25)/(2・10x)
=(75+x^2)/(20x)
になります。
これらから、
(108-x^2)/(24x)=(75+x^2)/(20x)
が成り立つので、これを整理して、
x^2=90
から
x=±3√10
で、
x>0なので、
x=3√10
と、先ほどの答えと一致しました。
続いて、[2]です。問題を再掲します。
「[2]箱の中に、1から9までの番号を1つずつ書いた9枚のカードが入っている。ただし、異なるカードには異なる番号が書かれているものとする。この箱から2枚のカードを同時に選び、小さい方の数をXとする。これらのカードを箱に戻して、再び2枚のカードを同時に選び、小さい方の数をYとする。X=Yである確率を求めよ。」
まず、下のような表を作りましょう。

▲表.2枚のカードに書かれている数とX(Y)をまとめました
この表は、選んだ2枚のカードに書かれている数aとbと、XまたはYの関係を表しています。
例えば、a=4、b=6を選んだとすると、そのうちの小さい方がXまたはYになるので、X(Y)=4になります。
そこで、この表からX(Y)がn(n=1,2,3・・・,9)になる確率を求めましょう。
9枚のカードから2枚を選ぶ場合の数は、
9×8=72(通り)
です。
一方、n=1,2,3,・・・、9になる場合の数は、表から、それぞれ、
n=1 16(通り)
n=2 14(通り)
n=3 12(通り)
n=4 10(通り)
n=5 8(通り)
n=6 6(通り)
n=7 4(通り)
n=8 2(通り)
n=9 0(通り)
です。
したがって、n=1,2,3,・・・,9になる確率は、それぞれ、
n=1 16/72
n=2 14/72
n=3 12/72
n=4 10/72
n=5 8/72
n=6 6/72
n=7 4/72
n=8 2/72
n=9 0/72
になります。
そして、X=Yとなるのは、XもYも同じnになるということなので、その確率Pは、
P=(16/72)^2+(14/72)^2+(12/72)^2+(10/72)^2+(8/72)^2+(6/72)^2+(4/72)^2+(2/72)^2+(0/72)^2
=(8/36)^2+(7/36)^2+(6/36)^2+(5/36)^2+(4/36)^2+(3/36)^2+(2/36)^2+(1/36)^2
=(64+49+36+25+16+9+4+1)/36^2
=204/36^2
=17/108
で、これが答えです。(2乗和の公式を使えば簡単に計算できます)
また、表を作らないのであれば、X(Y)=1,2,3,・・・,9になる確率を次のように計算できます。
つまり、X(Y)=1になる確率p(1)は、2枚のカードのうち1枚が1で、もう1枚が2,3,4,・・・、9のときなので、
p(1)=1/9×8/8×2=16/72
で、同様に、
p(2)=1/9×7/8×2=14/72
p(3)=1/9×6/8×2=12/72
・・・・・
p(9)=1/9×0/8×2= 0/72
となり、先ほどの途中結果と同じになります。
どちらも簡単な問題でした。










