こんにちは。東久留米市の学習塾塾長です。
昨日の天気予報通り、晴れて暖かい日になり、上着なしで教室に来ました。明日はもっと暖かくなるようで、春爛漫です。
さて、今回は平成25年度京大入試問題(前期、文系)です。
問題は、
「投げたとき表の出る確率と裏が出る確率が等しい硬貨を用意する。数直線上に石を置き、この硬貨を投げて表が出れば数直線上で原点に関して対称な点に石を移動し、裏が出れば数直線上で座標1の点に関して対称な点に石を移動する。
(1)石が座標xの点にあるとする。2回硬貨を投げたとき、石が座標xの点にある確率を求めよ。
(2)石が原点にあるとする。nを自然数とし、2n回硬貨を投げたとき、石が座標2nの点にある確率を求めよ。」
です。
表が出たときと裏がでたときの石の移動の様子を下の図に表しました。
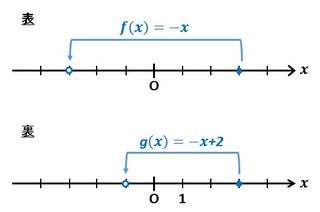
▲図.表のときと裏のときの石の移動です
ここで、石が座標xの点にあり、表が出たときの石の移動をf(x)、裏が出たときの石の移動をg(x)で表すと、
f(x)=-x [1]
g(x)=-x+2 [2]
になります。
そこで、(1)です。
硬貨を2回投げるので、その組合せは、f(f(x))、f(g(x))、g(f(x))、g(g(x))の4通りで、これらは(1)(2)から
f(f(x))=f(-x)=x [3]
f(g(x))=f(-x+2)=x-2 [4]
g(f(x))=g(-x)=x+2 [5]
g(g(x))=g(-x+2)=x [6]
になります。
つまり、石が座標xの点にあるのは、[3]と[6]の2通りなので、求める確率は2/4=1/2です。
続いて、(2)です。
まず、[3][4][5][6]での石の移動を調べてみましょう。
[3]と[4]は、石の座標をxからxに移動すること、つまり、石は動きません。
[5]は、石の座標をxからx+2に移動すること、つまり、石は数直線上を+方向に2だけ移動します。
[6]は、石の座標をxからx-2に移動すること、つまり、石は数直線上を-方向に2だけ移動します。
以上から、石が原点にあるときから始めて、硬貨を2n回投げ、つまり、[3][4][5][6]を合わせてn回作用させて、石を座標2nの点に移動させるためには、1回の作用で数直線上を+2ずつ移動させる以外に方法はなく、したがって、[5]をn回繰り返すことになります。
したがって、求める確率は(1/4)^n です。
(1)が(2)の誘導になっているので、一層簡単な問題でした。
昨日の天気予報通り、晴れて暖かい日になり、上着なしで教室に来ました。明日はもっと暖かくなるようで、春爛漫です。
さて、今回は平成25年度京大入試問題(前期、文系)です。
問題は、
「投げたとき表の出る確率と裏が出る確率が等しい硬貨を用意する。数直線上に石を置き、この硬貨を投げて表が出れば数直線上で原点に関して対称な点に石を移動し、裏が出れば数直線上で座標1の点に関して対称な点に石を移動する。
(1)石が座標xの点にあるとする。2回硬貨を投げたとき、石が座標xの点にある確率を求めよ。
(2)石が原点にあるとする。nを自然数とし、2n回硬貨を投げたとき、石が座標2nの点にある確率を求めよ。」
です。
表が出たときと裏がでたときの石の移動の様子を下の図に表しました。

▲図.表のときと裏のときの石の移動です
ここで、石が座標xの点にあり、表が出たときの石の移動をf(x)、裏が出たときの石の移動をg(x)で表すと、
f(x)=-x [1]
g(x)=-x+2 [2]
になります。
そこで、(1)です。
硬貨を2回投げるので、その組合せは、f(f(x))、f(g(x))、g(f(x))、g(g(x))の4通りで、これらは(1)(2)から
f(f(x))=f(-x)=x [3]
f(g(x))=f(-x+2)=x-2 [4]
g(f(x))=g(-x)=x+2 [5]
g(g(x))=g(-x+2)=x [6]
になります。
つまり、石が座標xの点にあるのは、[3]と[6]の2通りなので、求める確率は2/4=1/2です。
続いて、(2)です。
まず、[3][4][5][6]での石の移動を調べてみましょう。
[3]と[4]は、石の座標をxからxに移動すること、つまり、石は動きません。
[5]は、石の座標をxからx+2に移動すること、つまり、石は数直線上を+方向に2だけ移動します。
[6]は、石の座標をxからx-2に移動すること、つまり、石は数直線上を-方向に2だけ移動します。
以上から、石が原点にあるときから始めて、硬貨を2n回投げ、つまり、[3][4][5][6]を合わせてn回作用させて、石を座標2nの点に移動させるためには、1回の作用で数直線上を+2ずつ移動させる以外に方法はなく、したがって、[5]をn回繰り返すことになります。
したがって、求める確率は(1/4)^n です。
(1)が(2)の誘導になっているので、一層簡単な問題でした。










