こんにちは。東久留米市の学習塾塾長です。
明日からGWは、3日の憲法記念日と4日のみどりの日が曇りや雨模様ですが、その他は好天で、行楽日和の連休になりそうです。
さて、今回は平成28年度開成高校入試問題です。
問題は、6つの小問からなる大問1の1つで、
「次の連立方程式の解がないとき、定数aの値を求めよ。
 」
」
です。
まず、代数的に解いてみましょう。
2x+ay=a (1)
(-1+4a-a^2)x+ay=1 (2)
として、(1)-(2)から
(3-4a+a^2)x=a-1
(a-1)(a-3)x=a-1 (3)
です。
ここで、a=1のとき、(3)はどのようなxについても成り立つので、不定になります。
一方、a≠1のとき、(3)は、
(a-3)x=1 (4)
になり、ここで、a=3のとき、(4)の左辺は0、右辺は1で、(4)は成立せず、不能になります。
さらに、a≠3のとき、(4)から、
x=1/(a-3)
で、これを(1)に代入して、
2/(a-3)+ay=a
ay=a-2/(a-3) (5)
になります。
ここで、a=0のとき、(5)の左辺は0、右辺は2/3で、(5)は成立すず、不能になります。
以上から、与えられた連立方程式が解を持たないのは、a=0または3のときで、これが答えです。
続いて、2元1次連立方程式の解が平面上の2つの直線の交点になることを使って解いてみましょう。
(1)(2)もxy平面上の2直線を表しますが、(1)(2)が解を持たないということは、直線(1)、(2)が平行で、かつ一致しないということになります。
一方、直線px+qy=rとp’x+q’y=r’が平行で、かつ一致しない条件は、
p/p’=q/q’≠r/r’
です。
そこで、(1)(2)にこの条件を適用すると、
(-1+4a-a^2)/2=a/a≠1/a (6)
になります。
ここで、a≠0のとき、(6)の等式から
-1+4a-a^2=2
a^2-4a+3=0
(a-3)(a-1)=0
a=1、3
です。
ところが、a=1のとき、(6)の非等号(≠)の式が成り立たない(→1=1になってしまう)ので、直線(1)と(2)は一致します。
したがって、直線(1)と(2)が平行になるのはa=3のときで、2つの直線は、図1のようになります。

▲図1.a=3のときの2つの直線
一方、a=0のとき、(1)(2)はそれぞれ、
2x=0→x=0
-x=1→x=-1
になり、図2のように、直線(1)と(2)は平行で交点を持ちません。
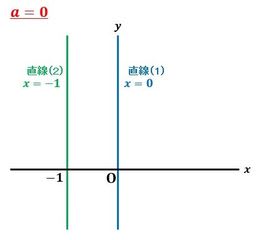
▲図2.a=0のときの2つの直線
以上から、与えられた連立方程式が解を持たないのは、a=0または3のときになります。
後半では、(1)(2)を馴染み深いy=Ax+Bのように変形して、それぞれの傾きが等しく切片が異なる、という条件で解いてもOKです。興味のある人は調べてみてください。
明日からGWは、3日の憲法記念日と4日のみどりの日が曇りや雨模様ですが、その他は好天で、行楽日和の連休になりそうです。
さて、今回は平成28年度開成高校入試問題です。
問題は、6つの小問からなる大問1の1つで、
「次の連立方程式の解がないとき、定数aの値を求めよ。
 」
」です。
まず、代数的に解いてみましょう。
2x+ay=a (1)
(-1+4a-a^2)x+ay=1 (2)
として、(1)-(2)から
(3-4a+a^2)x=a-1
(a-1)(a-3)x=a-1 (3)
です。
ここで、a=1のとき、(3)はどのようなxについても成り立つので、不定になります。
一方、a≠1のとき、(3)は、
(a-3)x=1 (4)
になり、ここで、a=3のとき、(4)の左辺は0、右辺は1で、(4)は成立せず、不能になります。
さらに、a≠3のとき、(4)から、
x=1/(a-3)
で、これを(1)に代入して、
2/(a-3)+ay=a
ay=a-2/(a-3) (5)
になります。
ここで、a=0のとき、(5)の左辺は0、右辺は2/3で、(5)は成立すず、不能になります。
以上から、与えられた連立方程式が解を持たないのは、a=0または3のときで、これが答えです。
続いて、2元1次連立方程式の解が平面上の2つの直線の交点になることを使って解いてみましょう。
(1)(2)もxy平面上の2直線を表しますが、(1)(2)が解を持たないということは、直線(1)、(2)が平行で、かつ一致しないということになります。
一方、直線px+qy=rとp’x+q’y=r’が平行で、かつ一致しない条件は、
p/p’=q/q’≠r/r’
です。
そこで、(1)(2)にこの条件を適用すると、
(-1+4a-a^2)/2=a/a≠1/a (6)
になります。
ここで、a≠0のとき、(6)の等式から
-1+4a-a^2=2
a^2-4a+3=0
(a-3)(a-1)=0
a=1、3
です。
ところが、a=1のとき、(6)の非等号(≠)の式が成り立たない(→1=1になってしまう)ので、直線(1)と(2)は一致します。
したがって、直線(1)と(2)が平行になるのはa=3のときで、2つの直線は、図1のようになります。

▲図1.a=3のときの2つの直線
一方、a=0のとき、(1)(2)はそれぞれ、
2x=0→x=0
-x=1→x=-1
になり、図2のように、直線(1)と(2)は平行で交点を持ちません。

▲図2.a=0のときの2つの直線
以上から、与えられた連立方程式が解を持たないのは、a=0または3のときになります。
後半では、(1)(2)を馴染み深いy=Ax+Bのように変形して、それぞれの傾きが等しく切片が異なる、という条件で解いてもOKです。興味のある人は調べてみてください。










