こんにちは。東久留米市の学習塾塾長です。
昨日と同様、いい天気になりました。昼過ぎに郵便局に行ったのですが、上着なしでも暑いくらいでした。明日からの3日間は曇りや雨のようですが、その後は晴れて、GWの前半は行楽日和になりそうです。
さて、前回まで平成28年度開成高入試の因数分解の問題を取り上げましたが、今回は、式の形が簡単なわりにあまり見かけない因数分解の問題です。
問題は、
「次の式を因数分解しなさい。
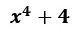 」
」
です。
与式の+が-であれば、よく見かける形で、

と和と差の積の形に簡単に因数分解できるのですが、与式の因数分解はあまり見かけません。
そこで、手元の公式集を調べてみると、複2次式の因数分解の方法が載っていて、そこには、

の形は、
(1)

とおいて、

の因数分解を考える。
(2)

のような2乗の差に導くことを考える、
とあります。
ここで、(1)は上手くいきそうもないので、(2)を調べてみると、
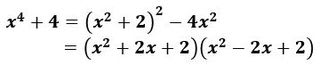
と上手く因数分解できます。
これは、

のように表すことができます。この形の式が因数分解できることを頭に入れておくと役に立つことがあるかも知れません。
昨日と同様、いい天気になりました。昼過ぎに郵便局に行ったのですが、上着なしでも暑いくらいでした。明日からの3日間は曇りや雨のようですが、その後は晴れて、GWの前半は行楽日和になりそうです。
さて、前回まで平成28年度開成高入試の因数分解の問題を取り上げましたが、今回は、式の形が簡単なわりにあまり見かけない因数分解の問題です。
問題は、
「次の式を因数分解しなさい。
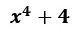 」
」です。
与式の+が-であれば、よく見かける形で、

と和と差の積の形に簡単に因数分解できるのですが、与式の因数分解はあまり見かけません。
そこで、手元の公式集を調べてみると、複2次式の因数分解の方法が載っていて、そこには、

の形は、
(1)

とおいて、

の因数分解を考える。
(2)

のような2乗の差に導くことを考える、
とあります。
ここで、(1)は上手くいきそうもないので、(2)を調べてみると、
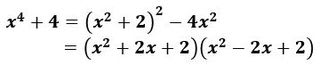
と上手く因数分解できます。
これは、

のように表すことができます。この形の式が因数分解できることを頭に入れておくと役に立つことがあるかも知れません。










