こんにちは。東久留米市の学習塾塾長です。
今回は、令和2年度灘中の問題です。
問題は、
「下の図は、1辺の長さが6cmの立方体ABCD-EFGHです。
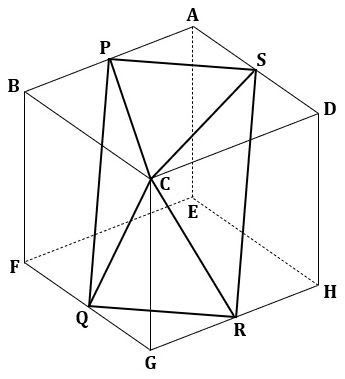
Pは辺ABの真ん中の点、Qは辺FGの真ん中の点、Rは辺GHの真ん中の点です。この立方体を3点P、Q、Rを通る平面で切ったとき、この平面は辺ADの真ん中の点Sを通ります。
(1) 四角すいC-PQRSの体積を求めなさい。
(2) 3点A、B、Gを通る平面で四角すいC-PQRSを2つの立体に分けたとき、点Qを含む方の立体の体積を求めなさい。
(3) 3点B、D、Fを通る平面で四角すいC-PQRSを2つの立体に分けたとき、その切り口の面積は、四角形BFHDの面積の[ ]倍で、点Qを含む方の立体の体積は[ ]cm3です。」
です。
図1に、与えられた条件を書き入れました。

▲図1.与えられた条件を書き入れました
中学生ならば、三平方の定理を利用して解けそうですが、ここではそれを使わずに進めましょう。
立方体を辺DHと辺BFが重なるように辺DH側から眺めると、平面PQRSは図2に緑色でマークした線分SRになり、立方体は、平面PQRSにより2等分されます。

▲図2.平面PQRSは辺DHの中点Yで交わります
また、平面PQRSは辺DH、辺BFの中点で交わり、したがって、立方体を平面PQRSで切ったときの切り口は、図3のように、正六角形PXQRYSになります。

▲図3.立方体を平面PQRSで切ったときの切り口は正六角形PXQRYSになります
ここで、正六角すいC-PXQRYSの体積は、立方体の体積の半分から、図4に示す3つの三角すいC-PBX、C-QGR、C-YDSの体積を引いたものなので、

です。

▲図4.正六角すいC-PXQRYSの体積は立方体の体積の半分から3つの三角すいC-PBX、C-QGR、C-YDSの体積を引いたものになります
このとき、正六角すいの底面の正六角形PXQRYSに注目すると、これは正六角形の中心と各頂点を結んだ6つの合同な正三角形から成り、この正六角形からら長方形PQRSを除いた図形は△XPQと△YRSで、これらの面積はいずれも正三角形の面積と等しくなります。
したがって、正六角形PXQRYSと長方形PQRSの面積比は6:4=3:2になり、これから、

で、これが(1)の答えです。
次に(2)です。
3点A、B、Gを通る平面は、図5の図のように、平面ABGH(青色でマーク)になり、直線PRはこの平面上にあります。

▲図5.直線PRは平面ABGH上にあります
ここで図6のように、直線BGと直線CQとの交点をZとすると、平面ABGHによって四角すいC-PQRSを2つの立体に分けたときの点Qを含む立体は、三角すいZ-PQR(赤色でマーク)になります。

▲図6.体積を求める立体は三角すいZ-PQRです
このとき、三角すいZ-PQRの底面PQRは、四角すいC-PQRSの底面PQRSの半分なので、三角すいZ-PQRと四角すいC-PQRSの高さの比が判れば、(1)の答えから三角すいZ-PQRの体積が計算できます。
そこで図6の右側の図のように、面BFGCに注目すると、△ZQG∽△ZBC、QG:CB=1:2から、ZQ:ZC=1:2になり、したがって、CQ:ZQ=3:1で、このとき四角すいC-PQRSと三角すいZ-PQRの高さの比はCOとZOの比に等しくなります。
したがって、

で、これが答えです。
最後の(3)です。
3点B、D、Fを通る平面は、図7の左側の図のように、平面BFHD(青色でマーク)になり、直線BDと直線XYはこの平面上にあります。
ここで直線BDと直線PCおよび直線SCとの交点をそれぞれT、U、さらに、直線XYと直線PQおよび直線SRとの交点をそれぞれV、Wとすると、平面BFHDによって四角すいC-PQRSを2つの立体に分けたときの切り口は、台形TVWU(紺色でマーク)になります。

▲図7.平面BFHDによって四角すいC-PQRSを2つの立体に分けたときの切り口は四角形TVWUです
そこで図7の右側の図のように、面ABCDに注目すると、△ABD∽△APS、AB:AP=2:1から、BD:PS=2:1で、このとき、BDの長さを2k(cm)とすると、PS=k(cm)です。
また、△CDT∽△PBT、CD:PB=2:1から、DT:BT=2:1になり、したがって、BD:BT=3:1で、同様に、BD:DU=3:1になることから、

です。
このとき、PS=VW=k(cm)から

です。
一方、
(長方形BFHDの面積)=2k×6=12k(cm2)
なので、台形TVWUの面積は長方形BFHDの面積の

です。
次に、平面BFHDによって四角すいC-PQRSを2つの立体に分けたときの点Qを含む方の立体の体積を計算します。
この立体は、図8のように、四角すいC-PQRSから立体PSWVTUを除いたものなので、ここでは立体PSWVTUの体積を求めて、それを四角すいC-PQRSの体積から差し引くことにします。

▲図8.立体PSWVTUは四角すいC-PVWSから四角すいC-TVWUを除いたものです
まず図8の右側の図のように、△CDT∽△PBT、CD:PT=2:1から、CT:TP=2:1、同様に、CU:US=2:1です。
次に図9のように、四角すいC-PQVWを2つの三角すいC-PVSとC-VWSに分けると、これらの2つの三角すいは合同で、

です。

▲図9.四角すいC-PQVWを2つの三角すいC-PVSとC-VWSに分けました
ここで図8の左側の図の三角すいC-PVSに注目すると、
(△CPSの面積):(台形PSUTの面積)=9:5
から、

です。
続いて図9の右側の図の三角すいC-VWSに注目すると、
(△CSWの面積):(△USWの面積)=3:1
から、

です。
したがって、

になり、平面BFHDによって四角すいC-PQRSを2つの立体に分けたときの点Qを含む方の立体の体積は、
(四角すいC-PQRSの体積)-(立体PSWVTUの体積)=54-12=42(cm3)
です。
以上をまとめると、1番目と2番目の[ ]は、それぞれ

で、これが答えです。
簡単な問題です。
今回は、令和2年度灘中の問題です。
問題は、
「下の図は、1辺の長さが6cmの立方体ABCD-EFGHです。

Pは辺ABの真ん中の点、Qは辺FGの真ん中の点、Rは辺GHの真ん中の点です。この立方体を3点P、Q、Rを通る平面で切ったとき、この平面は辺ADの真ん中の点Sを通ります。
(1) 四角すいC-PQRSの体積を求めなさい。
(2) 3点A、B、Gを通る平面で四角すいC-PQRSを2つの立体に分けたとき、点Qを含む方の立体の体積を求めなさい。
(3) 3点B、D、Fを通る平面で四角すいC-PQRSを2つの立体に分けたとき、その切り口の面積は、四角形BFHDの面積の[ ]倍で、点Qを含む方の立体の体積は[ ]cm3です。」
です。
図1に、与えられた条件を書き入れました。

▲図1.与えられた条件を書き入れました
中学生ならば、三平方の定理を利用して解けそうですが、ここではそれを使わずに進めましょう。
立方体を辺DHと辺BFが重なるように辺DH側から眺めると、平面PQRSは図2に緑色でマークした線分SRになり、立方体は、平面PQRSにより2等分されます。

▲図2.平面PQRSは辺DHの中点Yで交わります
また、平面PQRSは辺DH、辺BFの中点で交わり、したがって、立方体を平面PQRSで切ったときの切り口は、図3のように、正六角形PXQRYSになります。

▲図3.立方体を平面PQRSで切ったときの切り口は正六角形PXQRYSになります
ここで、正六角すいC-PXQRYSの体積は、立方体の体積の半分から、図4に示す3つの三角すいC-PBX、C-QGR、C-YDSの体積を引いたものなので、

です。

▲図4.正六角すいC-PXQRYSの体積は立方体の体積の半分から3つの三角すいC-PBX、C-QGR、C-YDSの体積を引いたものになります
このとき、正六角すいの底面の正六角形PXQRYSに注目すると、これは正六角形の中心と各頂点を結んだ6つの合同な正三角形から成り、この正六角形からら長方形PQRSを除いた図形は△XPQと△YRSで、これらの面積はいずれも正三角形の面積と等しくなります。
したがって、正六角形PXQRYSと長方形PQRSの面積比は6:4=3:2になり、これから、

で、これが(1)の答えです。
次に(2)です。
3点A、B、Gを通る平面は、図5の図のように、平面ABGH(青色でマーク)になり、直線PRはこの平面上にあります。

▲図5.直線PRは平面ABGH上にあります
ここで図6のように、直線BGと直線CQとの交点をZとすると、平面ABGHによって四角すいC-PQRSを2つの立体に分けたときの点Qを含む立体は、三角すいZ-PQR(赤色でマーク)になります。

▲図6.体積を求める立体は三角すいZ-PQRです
このとき、三角すいZ-PQRの底面PQRは、四角すいC-PQRSの底面PQRSの半分なので、三角すいZ-PQRと四角すいC-PQRSの高さの比が判れば、(1)の答えから三角すいZ-PQRの体積が計算できます。
そこで図6の右側の図のように、面BFGCに注目すると、△ZQG∽△ZBC、QG:CB=1:2から、ZQ:ZC=1:2になり、したがって、CQ:ZQ=3:1で、このとき四角すいC-PQRSと三角すいZ-PQRの高さの比はCOとZOの比に等しくなります。
したがって、

で、これが答えです。
最後の(3)です。
3点B、D、Fを通る平面は、図7の左側の図のように、平面BFHD(青色でマーク)になり、直線BDと直線XYはこの平面上にあります。
ここで直線BDと直線PCおよび直線SCとの交点をそれぞれT、U、さらに、直線XYと直線PQおよび直線SRとの交点をそれぞれV、Wとすると、平面BFHDによって四角すいC-PQRSを2つの立体に分けたときの切り口は、台形TVWU(紺色でマーク)になります。

▲図7.平面BFHDによって四角すいC-PQRSを2つの立体に分けたときの切り口は四角形TVWUです
そこで図7の右側の図のように、面ABCDに注目すると、△ABD∽△APS、AB:AP=2:1から、BD:PS=2:1で、このとき、BDの長さを2k(cm)とすると、PS=k(cm)です。
また、△CDT∽△PBT、CD:PB=2:1から、DT:BT=2:1になり、したがって、BD:BT=3:1で、同様に、BD:DU=3:1になることから、

です。
このとき、PS=VW=k(cm)から

です。
一方、
(長方形BFHDの面積)=2k×6=12k(cm2)
なので、台形TVWUの面積は長方形BFHDの面積の

です。
次に、平面BFHDによって四角すいC-PQRSを2つの立体に分けたときの点Qを含む方の立体の体積を計算します。
この立体は、図8のように、四角すいC-PQRSから立体PSWVTUを除いたものなので、ここでは立体PSWVTUの体積を求めて、それを四角すいC-PQRSの体積から差し引くことにします。

▲図8.立体PSWVTUは四角すいC-PVWSから四角すいC-TVWUを除いたものです
まず図8の右側の図のように、△CDT∽△PBT、CD:PT=2:1から、CT:TP=2:1、同様に、CU:US=2:1です。
次に図9のように、四角すいC-PQVWを2つの三角すいC-PVSとC-VWSに分けると、これらの2つの三角すいは合同で、

です。

▲図9.四角すいC-PQVWを2つの三角すいC-PVSとC-VWSに分けました
ここで図8の左側の図の三角すいC-PVSに注目すると、
(△CPSの面積):(台形PSUTの面積)=9:5
から、

です。
続いて図9の右側の図の三角すいC-VWSに注目すると、
(△CSWの面積):(△USWの面積)=3:1
から、

です。
したがって、

になり、平面BFHDによって四角すいC-PQRSを2つの立体に分けたときの点Qを含む方の立体の体積は、
(四角すいC-PQRSの体積)-(立体PSWVTUの体積)=54-12=42(cm3)
です。
以上をまとめると、1番目と2番目の[ ]は、それぞれ

で、これが答えです。
簡単な問題です。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます