こんにちは。東久留米市の学習塾塾長です。
雲があって、時々陽射しが弱くなりますが、風はなく過ごしやすい日になりました。明日、明後日は同じような天気になりますが、明々後日には南岸低気圧が近づいて、真冬のような寒さになるようです。
さて、今回は直角三角形の辺の比についてです。
図1のような、三角定規の2つの直角三角形の辺の比は、三平方の定理から導くことができますが、定期考査や入試で頻出なので、覚えておくほうがいでしょう。
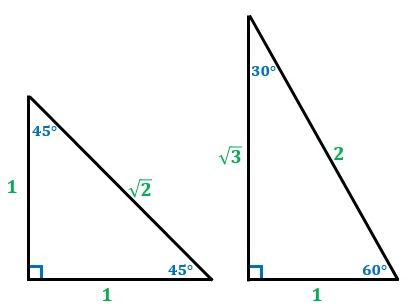
▲図1.三角定規の2つの直角三角形の辺の比
さらに、難関高校の入試問題には、図2のような、内角が15°、75°、90°の直角三角形の辺の比を利用するものもあります。
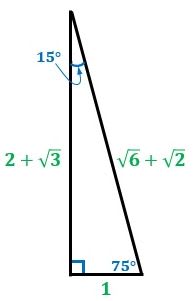
▲図2.内角が15°、75°、90°の直角三角形の辺の比
ところが、この直角三角形の辺の比は、三角定規の2つの直角三角形の辺の比に比べて、単純ではなく、おまけに頻出ではないので、忘れてしまいがちです。(私は覚えていません)
そこで今回は、この直角三角形の辺の比の導き方を紹介したいと思います。
まず図3のような内角が30°、60°、90°の直角三角形ABCの辺ABを、Aの方向に辺ACの長さ延長し、その端点をDとします。
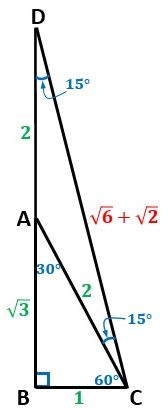
▲図3.直角三角形ABCの辺ABを、Aの方向に辺ACの長さ延長し、その端点をDとしました
そこで、CとDを結ぶと、△ACDは二等辺三角形で、∠CAD=150°なので、∠ACD=∠ADC=15°です。
つまり、△DBCは内角が15°、75°、90°の直角三角形になります。
ここで、△ABCの辺の長さを、AB=√3、BC=1、CA=2とすると、AD=2なので、DB=2+√3です。
そこで、直角三角形DBCに三平方の定理を適用すると、
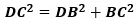
が成り立ち、これに、DB=2+√3、BC=1を代入して、
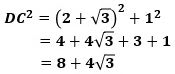
から、
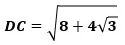
です。
最後に、右辺の二重根号を外すと、(因数分解と同じ要領です)
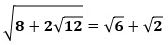
になり、
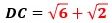
です。
以上から、内角が15°、75°、90°の辺の比は、1 : 2+√3 : √6+√2 になります。
他にも、△ABCで∠Aの2等分線を引き、角の2等分定理を利用しても求めることができます。
次回は、内角が15°、75°、90°の直角三角形の辺の比を利用する京大入試問題を取り上げます。
雲があって、時々陽射しが弱くなりますが、風はなく過ごしやすい日になりました。明日、明後日は同じような天気になりますが、明々後日には南岸低気圧が近づいて、真冬のような寒さになるようです。
さて、今回は直角三角形の辺の比についてです。
図1のような、三角定規の2つの直角三角形の辺の比は、三平方の定理から導くことができますが、定期考査や入試で頻出なので、覚えておくほうがいでしょう。

▲図1.三角定規の2つの直角三角形の辺の比
さらに、難関高校の入試問題には、図2のような、内角が15°、75°、90°の直角三角形の辺の比を利用するものもあります。

▲図2.内角が15°、75°、90°の直角三角形の辺の比
ところが、この直角三角形の辺の比は、三角定規の2つの直角三角形の辺の比に比べて、単純ではなく、おまけに頻出ではないので、忘れてしまいがちです。(私は覚えていません)
そこで今回は、この直角三角形の辺の比の導き方を紹介したいと思います。
まず図3のような内角が30°、60°、90°の直角三角形ABCの辺ABを、Aの方向に辺ACの長さ延長し、その端点をDとします。

▲図3.直角三角形ABCの辺ABを、Aの方向に辺ACの長さ延長し、その端点をDとしました
そこで、CとDを結ぶと、△ACDは二等辺三角形で、∠CAD=150°なので、∠ACD=∠ADC=15°です。
つまり、△DBCは内角が15°、75°、90°の直角三角形になります。
ここで、△ABCの辺の長さを、AB=√3、BC=1、CA=2とすると、AD=2なので、DB=2+√3です。
そこで、直角三角形DBCに三平方の定理を適用すると、
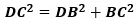
が成り立ち、これに、DB=2+√3、BC=1を代入して、
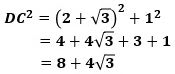
から、
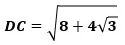
です。
最後に、右辺の二重根号を外すと、(因数分解と同じ要領です)
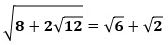
になり、
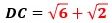
です。
以上から、内角が15°、75°、90°の辺の比は、1 : 2+√3 : √6+√2 になります。
他にも、△ABCで∠Aの2等分線を引き、角の2等分定理を利用しても求めることができます。
次回は、内角が15°、75°、90°の直角三角形の辺の比を利用する京大入試問題を取り上げます。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます