こんにちは。東久留米市の学習塾塾長です。
今回は、2020年日本ジュニア数学オリンピック予選の問題です。
問題は、
「一辺の長さが1の正六角形の形をした盤面がある。盤面を図のように一辺の長さ

の正三角形に分割したとき、図において〇で示されている19個の点を良い点とよぶ。
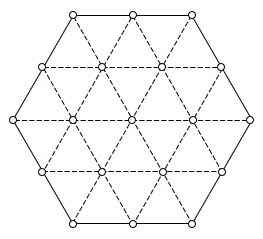
3辺の長さが

であるような直角三角形の形をしたタイルが12枚あり、盤面に重ならないように置いて全体を覆う。このようなタイルの置き方のうち、次の条件をみたすものは何通りか。
(i) 置かれたタイルの頂点はすべて、良い点と重なっている。
(ii) ちょうど2枚のタイルからなる一辺の長さが1の正三角形は現れない。
ただし、タイルは回転したり裏返したりしてもよいが、盤面を回転したり裏返したりして一致する置き方は区別して数える。」
です。
早速、取り掛かりましょう。
3辺の長さが

の直角三角形のタイルを2枚組合せることを考えます。
図1のように、長さ
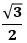
の辺と他の2辺がそれぞれ重なる場合、AとBが良い点に一致する可能性があるように置く

と、Cは良い点と一致することはなく、これは条件(i)に反します。

▲図1.2枚のタイルの置き方(1)
また図2のように、長さ
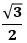
の辺同士が重なる場合、直角の角が並ぶ置き方は1辺の長さが1の正三角形になり、これは条件(ii)に反します。

▲図2.2枚のタイルの置き方(2)
したがって、2枚のタイルは、図2の中央図に示す平行四辺形のように置かれ、この置き方は1通りです。
さらに、この2枚のタイルを組合わせた平行四辺形を2組並べて1辺の長さが1のひし形を作るとき、平行四辺形の置き方は、図3のように、2通りになります。

▲図3.1辺の長さが1のひし形を作るとき、平行四辺形の置き方は2通りです
これで準備完了です。ここから正六角形の盤面に平行四辺形とひし形を置いていきます。
このとき、ひし形と正六角形の盤面の中心との位置関係は、
① ひし形の内部(周上を含めない)に正六角形の盤面の中心がある
② ひし形の周上(頂点を含めない)に正六角形の盤面の中心がある
③ ひし形の頂点に正六角形の盤面の中心がある
④ ひし形の外部(周上を含めない)に正六角形の盤面の中心がある
⑤ ひし形を正六角形の盤面に置かない
の5つの場合になりますが、ひし形を②、④、⑤のように置くことはできません。
したがって、ここでは①と③の場合について調べます。
① ひし形の内部(周上を含めない)に正六角形の盤面の中心がある場合
図4のように、ひし形の置き方は3通りです。

▲図4.ひし形の置き方は3通りです
このとき、1つのひし形に対して平行四辺形の置き方は2通りで、さらにひし形の周りの平行四辺形の置き方は1通りなので、ひし形の内部(周上を含めない)に正六角形の盤面の中心がある場合のタイルの置き方は、
2×1×3=6(通り)
です。
③ ひし形の頂点に正六角形の盤面の中心がある場合
図5のように、ひし形の置き方は2通りです。
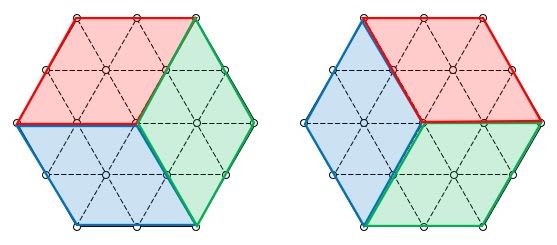
▲図5.ひし形の置き方は2通りです
このとき、3つのひし形それぞれに対して平行四辺形の置き方は2通りなので、ひし形の頂点に正六角形の盤面の中心がある場合のタイルの置き方は、
2×2×2×2=16(通り)
です。
以上から、与えられた条件をみたすタイルの置き方は、
6+16= 22(通り)
で、これが答えです。
簡単な問題です。
今回は、2020年日本ジュニア数学オリンピック予選の問題です。
問題は、
「一辺の長さが1の正六角形の形をした盤面がある。盤面を図のように一辺の長さ

の正三角形に分割したとき、図において〇で示されている19個の点を良い点とよぶ。

3辺の長さが

であるような直角三角形の形をしたタイルが12枚あり、盤面に重ならないように置いて全体を覆う。このようなタイルの置き方のうち、次の条件をみたすものは何通りか。
(i) 置かれたタイルの頂点はすべて、良い点と重なっている。
(ii) ちょうど2枚のタイルからなる一辺の長さが1の正三角形は現れない。
ただし、タイルは回転したり裏返したりしてもよいが、盤面を回転したり裏返したりして一致する置き方は区別して数える。」
です。
早速、取り掛かりましょう。
3辺の長さが

の直角三角形のタイルを2枚組合せることを考えます。
図1のように、長さ
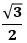
の辺と他の2辺がそれぞれ重なる場合、AとBが良い点に一致する可能性があるように置く

と、Cは良い点と一致することはなく、これは条件(i)に反します。

▲図1.2枚のタイルの置き方(1)
また図2のように、長さ
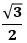
の辺同士が重なる場合、直角の角が並ぶ置き方は1辺の長さが1の正三角形になり、これは条件(ii)に反します。

▲図2.2枚のタイルの置き方(2)
したがって、2枚のタイルは、図2の中央図に示す平行四辺形のように置かれ、この置き方は1通りです。
さらに、この2枚のタイルを組合わせた平行四辺形を2組並べて1辺の長さが1のひし形を作るとき、平行四辺形の置き方は、図3のように、2通りになります。

▲図3.1辺の長さが1のひし形を作るとき、平行四辺形の置き方は2通りです
これで準備完了です。ここから正六角形の盤面に平行四辺形とひし形を置いていきます。
このとき、ひし形と正六角形の盤面の中心との位置関係は、
① ひし形の内部(周上を含めない)に正六角形の盤面の中心がある
② ひし形の周上(頂点を含めない)に正六角形の盤面の中心がある
③ ひし形の頂点に正六角形の盤面の中心がある
④ ひし形の外部(周上を含めない)に正六角形の盤面の中心がある
⑤ ひし形を正六角形の盤面に置かない
の5つの場合になりますが、ひし形を②、④、⑤のように置くことはできません。
したがって、ここでは①と③の場合について調べます。
① ひし形の内部(周上を含めない)に正六角形の盤面の中心がある場合
図4のように、ひし形の置き方は3通りです。

▲図4.ひし形の置き方は3通りです
このとき、1つのひし形に対して平行四辺形の置き方は2通りで、さらにひし形の周りの平行四辺形の置き方は1通りなので、ひし形の内部(周上を含めない)に正六角形の盤面の中心がある場合のタイルの置き方は、
2×1×3=6(通り)
です。
③ ひし形の頂点に正六角形の盤面の中心がある場合
図5のように、ひし形の置き方は2通りです。

▲図5.ひし形の置き方は2通りです
このとき、3つのひし形それぞれに対して平行四辺形の置き方は2通りなので、ひし形の頂点に正六角形の盤面の中心がある場合のタイルの置き方は、
2×2×2×2=16(通り)
です。
以上から、与えられた条件をみたすタイルの置き方は、
6+16= 22(通り)
で、これが答えです。
簡単な問題です。










