こんにちは。東久留米市の学習塾塾長です。
今回は、令和2年度灘高の問題です。
問題は、
「サイコロを3回投げる。1回目、2回目、3回目に出た目の数をそれぞれ百の位、十の位、一の位の数字とする整数を作る。
(1) この整数が、2の倍数または5の倍数となる確率を求めよ。
(2) この整数が、2の倍数または5の倍数または9の倍数となる確率を求めよ。」
です。
与えられた操作で作った整数が2の倍数になるのは、
・ 1、2投目の数がそれぞれ1から6までのいずれかの数
かつ、
・ 3投目の数が2、4、6
の場合なので、この場合の数は、
6×6×3=108(通り)
です。
また、5の倍数になるのは、
・ 1,2投目の数がそれぞれ1から6までのいずれかの数
かつ、
・ 3投目の数が5
の場合なので、この場合の数は、
6×6×1=36(通り)
です。
このとき、2の倍数と5の倍数に共通する整数は10の倍数ですが、サイコロの目の数に0はないので、10の倍数はありません。
したがって、2の倍数または5の倍数となる場合の数は、
108+36=144(通り)
で、このとき、すべての目の数の出方が
6×6×6=216(通り)
であることから、2の倍数または5の倍数となる確率は、
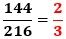
で、これが(1)の答えです。
続いて(2)です。
図1に示すベン図を考えましょう。
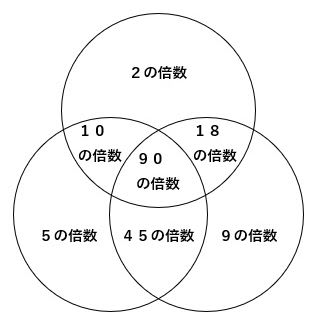
▲図1.ベン図を描きました
10の倍数の場合と同じように、90の倍数もありません。これと(1)の結果をベン図に書き入れると図2のようになります。

▲図2.(1)の結果と90の倍数の個数を書き入れました
ここからまず、9の倍数の個数を勘定します。
ある整数が9の倍数であると、整数の各桁の数の和は9の倍数になります。
また、サイコロの目の数は1以上6以下の整数なので、与えられた操作で作った整数の各桁の和は3以上18以下になり、このうち9の倍数は
9と18です。
したがって、サイコロを3回投げて出た目の和が9または18になる場合の数を勘定すればよく、ここから、それぞれの場合に分けて調べていきます。
● サイコロを3回投げて出た目の和が9の場合
9個の玉を左右1列に並べて、これらの8か所の間隔に2個の仕切りを入れ、左側の玉の個数を1投目の数、中央の玉の個数を2投目の数、右側の玉の数を3投目の数とします。
すると、この仕切りの入れ方のうち、仕切られた玉の個数が7個でないものの場合の数が、サイコロを3回投げて出た目の和が9になる整数の個数になります。
そこで、2個の仕切りの入れ方の場合の数を計算すると、

になり、このうち、仕切られた玉の個数が7個であるものの場合の数は、
〇〇〇〇〇〇〇l〇l〇
〇l〇〇〇〇〇〇〇l〇
〇l〇l〇〇〇〇〇〇〇
(〇:玉、 l:仕切り)
の3通りです。
したがって、サイコロを3回投げて出た目の和が9になる場合の数は、
28-3=25(通り)
です。
● サイコロを3回投げて出た目の和が18の場合
1投目、2投目、3投目の数がいずれも6のときなので、この場合の数は1通りです。
以上から、9の倍数の個数は、
25+1=26(個)
で、これを図3に書き入れました。

▲図3.9の倍数の個数は26個です
次に、18の倍数の個数を勘定します。
与えられた操作で作った整数が18の倍数になるのは、
① 3投目の数が2で1投目と2投目の数の和が7
② 3投目の数が4で1投目と2投目の数の和が5
③ 3投目の数が6で1投目と2投目の数の和が3または12
の場合です。
ここから、①、②、③のそれぞれの場合を調べます。
● ①の場合
3投目の数が2なので、1個の仕切りの位置は、
〇〇〇〇〇〇〇l〇〇
です。
すると①の場合の数は、1個目の仕切りの左側にある7個の玉の間隔(6か所)に2個目の仕切りを入れる場合の数になるので、

です。
● ②の場合
3投目の数が4なので、1個の仕切りの位置は、
〇〇〇〇〇l〇〇〇〇
です。
すると②の場合の数は、1個目の仕切りの左側にある5個の玉の間隔(4か所)に2個目の仕切りを入れる場合の数になるので、

です。
● ③の場合
3投目の数が6なので、1個の仕切りの位置は、
〇〇〇l〇〇〇〇〇〇
または
〇〇〇〇〇〇〇〇〇〇〇〇l〇〇〇〇〇〇
です。
すると③の場合の数は、〈上のとき〉1個目の仕切りの左側にある3個の玉の間隔(2か所)に2個目の仕切りを入れる場合の数になるので、

と、〈下のとき〉
〇〇〇〇〇〇l〇〇〇〇〇〇l〇〇〇〇〇〇
の1通りで、合わせて
2+1=3(通り)
です。
したがって、18の倍数の個数は、
6+4+2+1=13(個)
です。
続いて45の倍数の個数を勘定します。
与えられた操作で作った整数が45の倍数になるのは、
④ 3投目の数が5で1投目と2投目の数の和が4
の場合です。
● ④の場合
3投目の数が5なので、1個の仕切りの位置は、
〇〇〇〇l〇〇〇〇〇
です。
すると④の場合の数は、1個目の仕切りの左側にある4個の玉の間隔(3か所)に2個目の仕切りを入れる場合の数になるので、

です。
したがって、45の倍数の個数は、
3(個)
です。
これらをベン図に書き入れると図4のようになります。

▲図4.18と45の倍数の個数を書き入れました
ここで図5のように、ベン図の7個の領域にその個数を書き入れて完成です。

▲図5.ベン図が完成しました
図5から2の倍数または5の倍数または9の倍数の個数は、
95+33+10+0+13+3+0=154(個)
になり、したがって、2の倍数または5の倍数または9の倍数となる確率は、
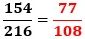
で、これが答えです。
簡単な問題です。
今回は、令和2年度灘高の問題です。
問題は、
「サイコロを3回投げる。1回目、2回目、3回目に出た目の数をそれぞれ百の位、十の位、一の位の数字とする整数を作る。
(1) この整数が、2の倍数または5の倍数となる確率を求めよ。
(2) この整数が、2の倍数または5の倍数または9の倍数となる確率を求めよ。」
です。
与えられた操作で作った整数が2の倍数になるのは、
・ 1、2投目の数がそれぞれ1から6までのいずれかの数
かつ、
・ 3投目の数が2、4、6
の場合なので、この場合の数は、
6×6×3=108(通り)
です。
また、5の倍数になるのは、
・ 1,2投目の数がそれぞれ1から6までのいずれかの数
かつ、
・ 3投目の数が5
の場合なので、この場合の数は、
6×6×1=36(通り)
です。
このとき、2の倍数と5の倍数に共通する整数は10の倍数ですが、サイコロの目の数に0はないので、10の倍数はありません。
したがって、2の倍数または5の倍数となる場合の数は、
108+36=144(通り)
で、このとき、すべての目の数の出方が
6×6×6=216(通り)
であることから、2の倍数または5の倍数となる確率は、
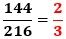
で、これが(1)の答えです。
続いて(2)です。
図1に示すベン図を考えましょう。

▲図1.ベン図を描きました
10の倍数の場合と同じように、90の倍数もありません。これと(1)の結果をベン図に書き入れると図2のようになります。

▲図2.(1)の結果と90の倍数の個数を書き入れました
ここからまず、9の倍数の個数を勘定します。
ある整数が9の倍数であると、整数の各桁の数の和は9の倍数になります。
また、サイコロの目の数は1以上6以下の整数なので、与えられた操作で作った整数の各桁の和は3以上18以下になり、このうち9の倍数は
9と18です。
したがって、サイコロを3回投げて出た目の和が9または18になる場合の数を勘定すればよく、ここから、それぞれの場合に分けて調べていきます。
● サイコロを3回投げて出た目の和が9の場合
9個の玉を左右1列に並べて、これらの8か所の間隔に2個の仕切りを入れ、左側の玉の個数を1投目の数、中央の玉の個数を2投目の数、右側の玉の数を3投目の数とします。
すると、この仕切りの入れ方のうち、仕切られた玉の個数が7個でないものの場合の数が、サイコロを3回投げて出た目の和が9になる整数の個数になります。
そこで、2個の仕切りの入れ方の場合の数を計算すると、

になり、このうち、仕切られた玉の個数が7個であるものの場合の数は、
〇〇〇〇〇〇〇l〇l〇
〇l〇〇〇〇〇〇〇l〇
〇l〇l〇〇〇〇〇〇〇
(〇:玉、 l:仕切り)
の3通りです。
したがって、サイコロを3回投げて出た目の和が9になる場合の数は、
28-3=25(通り)
です。
● サイコロを3回投げて出た目の和が18の場合
1投目、2投目、3投目の数がいずれも6のときなので、この場合の数は1通りです。
以上から、9の倍数の個数は、
25+1=26(個)
で、これを図3に書き入れました。

▲図3.9の倍数の個数は26個です
次に、18の倍数の個数を勘定します。
与えられた操作で作った整数が18の倍数になるのは、
① 3投目の数が2で1投目と2投目の数の和が7
② 3投目の数が4で1投目と2投目の数の和が5
③ 3投目の数が6で1投目と2投目の数の和が3または12
の場合です。
ここから、①、②、③のそれぞれの場合を調べます。
● ①の場合
3投目の数が2なので、1個の仕切りの位置は、
〇〇〇〇〇〇〇l〇〇
です。
すると①の場合の数は、1個目の仕切りの左側にある7個の玉の間隔(6か所)に2個目の仕切りを入れる場合の数になるので、

です。
● ②の場合
3投目の数が4なので、1個の仕切りの位置は、
〇〇〇〇〇l〇〇〇〇
です。
すると②の場合の数は、1個目の仕切りの左側にある5個の玉の間隔(4か所)に2個目の仕切りを入れる場合の数になるので、

です。
● ③の場合
3投目の数が6なので、1個の仕切りの位置は、
〇〇〇l〇〇〇〇〇〇
または
〇〇〇〇〇〇〇〇〇〇〇〇l〇〇〇〇〇〇
です。
すると③の場合の数は、〈上のとき〉1個目の仕切りの左側にある3個の玉の間隔(2か所)に2個目の仕切りを入れる場合の数になるので、

と、〈下のとき〉
〇〇〇〇〇〇l〇〇〇〇〇〇l〇〇〇〇〇〇
の1通りで、合わせて
2+1=3(通り)
です。
したがって、18の倍数の個数は、
6+4+2+1=13(個)
です。
続いて45の倍数の個数を勘定します。
与えられた操作で作った整数が45の倍数になるのは、
④ 3投目の数が5で1投目と2投目の数の和が4
の場合です。
● ④の場合
3投目の数が5なので、1個の仕切りの位置は、
〇〇〇〇l〇〇〇〇〇
です。
すると④の場合の数は、1個目の仕切りの左側にある4個の玉の間隔(3か所)に2個目の仕切りを入れる場合の数になるので、

です。
したがって、45の倍数の個数は、
3(個)
です。
これらをベン図に書き入れると図4のようになります。

▲図4.18と45の倍数の個数を書き入れました
ここで図5のように、ベン図の7個の領域にその個数を書き入れて完成です。

▲図5.ベン図が完成しました
図5から2の倍数または5の倍数または9の倍数の個数は、
95+33+10+0+13+3+0=154(個)
になり、したがって、2の倍数または5の倍数または9の倍数となる確率は、
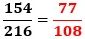
で、これが答えです。
簡単な問題です。










