こんにちは。東久留米市の学習塾塾長です。
今回は簡単な図形問題を取り上げます。
問題は、
「下図のように、△ABCの外接円の弧AB、BC、CAの中点をそれぞれD、E、Fとし、弦AEと弦DFの交点をXとするとき、∠AXDの角度を求めなさい」
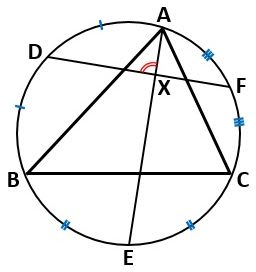
▲問題図
です。
3組の長さの等しい弧があるので、円周角の定理が活躍しそうです。そこで図1のように、AとD、AとFを直線で結ぶと、
弧AD=弧DB ⇒ ∠AFD=∠DAB (1)
弧AF=弧FC ⇒ ∠ADF=∠FAC (2)
弧BE=弧EC ⇒ ∠BAE=∠EAC (3)
が成り立ちます。

▲図1.∠AFD=∠DAB、∠ADF=∠FAC、∠BAE=∠EACです
次に図2のように、弦DFと辺AB、ACとの交点をそれぞれY、Zとすると、
∠AYZ=∠DAY+∠ADY [三角形の外角=それと隣合わない内角の和]
=∠DAB+∠ADF
=∠AFD+∠FAC [(1)と(2)]
=∠AFZ+∠FAZ
=∠AZY [三角形の外角=それと隣合わない内角の和]
になり、△AYZは二等辺三角形です。

▲図2.∠AYZ=∠AZYで、△AYZは二等辺三角形です
さらに、(3)から
∠YAX=∠XAZ
なので、直線AXは∠YAZの二等分線になり、二等辺三角形の頂角の二等分線は底辺に垂直に交わるので、
∠AXY=90°
です。
したがって、∠AXD= 90° で、これが答えです。
中3生がこれから勉強する円周角の定理は、都立高校入試に頻出なので、しっかりマスターしましょう。
今回は簡単な図形問題を取り上げます。
問題は、
「下図のように、△ABCの外接円の弧AB、BC、CAの中点をそれぞれD、E、Fとし、弦AEと弦DFの交点をXとするとき、∠AXDの角度を求めなさい」

▲問題図
です。
3組の長さの等しい弧があるので、円周角の定理が活躍しそうです。そこで図1のように、AとD、AとFを直線で結ぶと、
弧AD=弧DB ⇒ ∠AFD=∠DAB (1)
弧AF=弧FC ⇒ ∠ADF=∠FAC (2)
弧BE=弧EC ⇒ ∠BAE=∠EAC (3)
が成り立ちます。

▲図1.∠AFD=∠DAB、∠ADF=∠FAC、∠BAE=∠EACです
次に図2のように、弦DFと辺AB、ACとの交点をそれぞれY、Zとすると、
∠AYZ=∠DAY+∠ADY [三角形の外角=それと隣合わない内角の和]
=∠DAB+∠ADF
=∠AFD+∠FAC [(1)と(2)]
=∠AFZ+∠FAZ
=∠AZY [三角形の外角=それと隣合わない内角の和]
になり、△AYZは二等辺三角形です。

▲図2.∠AYZ=∠AZYで、△AYZは二等辺三角形です
さらに、(3)から
∠YAX=∠XAZ
なので、直線AXは∠YAZの二等分線になり、二等辺三角形の頂角の二等分線は底辺に垂直に交わるので、
∠AXY=90°
です。
したがって、∠AXD= 90° で、これが答えです。
中3生がこれから勉強する円周角の定理は、都立高校入試に頻出なので、しっかりマスターしましょう。










