こんにちは。東久留米市の学習塾塾長です。
今回は、平成31年度都立日比谷高入試問題を取り上げます。
問題は、
「下の図1に示した立体ABCD-EFGHは1辺の長さが6cmの立方体である。
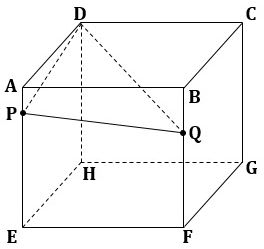
▲図1.問題図(1)
辺AE上にある点をP、辺BF上にある点をQとする。
頂点Dと点P、点Pと頂点Dをそれぞれ結ぶ。
次の各問に答えよ。
〔問1〕 AP=1cm、BQ=2cmのとき、△DPQの面積は何cm2か。
〔問2〕 頂点Cと点Q、頂点Cと点Pをそれぞれ結んだ場合を考える。
AP=a cm(0<a<6)とする。
直線DQと直線CPが交わるとき、立体APD-BQCの体積をaを用いた式で表せ。
ただし、答えだけではなく、答えを求める過程がわかるように、途中の式や計算なども書け。
〔問3〕 下の図2は、図1において、点Qが頂点Bの位置にあり、頂点Gと頂点D、頂点Gと点P、頂点Gと点Qをそれぞれ結んだ場合を表している。
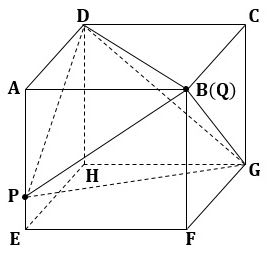
▲図2.問題図(2)
立体A-DPQの体積をVcm3、立体G-DPQの体積をWcm3とする。
AP=5cmのとき、V:Wを最も簡単な整数の比で表せ。」
です。
△ADPに三平方の定理を適用すると、
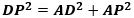
が成り立ち、これにAD=6cm、AP=1cmを代入すると、
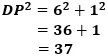
から、図3の左側のように、
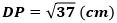
になります。
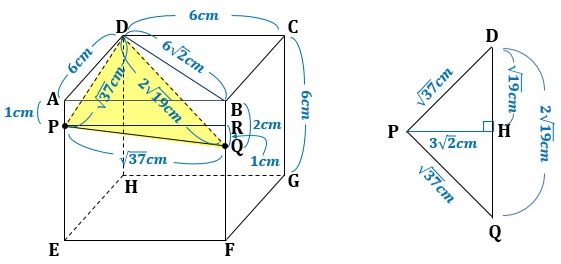
▲図3.△ADPに三平方の定理を適用しました
また、Pから辺BFに下ろした垂線の足をRとすると、△ADP≡△RPQ(AD=RP、AP=RQ、∠DAP=∠PRQ)になり、したがって、
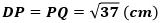
です。
続いて△BDQに三平方の定理を適用すると、
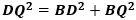
が成り立ち、このときBDは1辺6cmの正方形の対角線なので
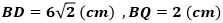
から
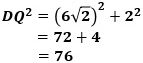
で、したがって、
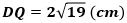
になり、これから△DPQは図3の右側に示すような二等辺三角形になります。
ここで、Pから線分DQに下ろした垂線の足をHとして、△PDHに三平方の定理を適用すると、
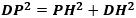
が成り立ち、これに
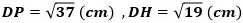
を代入すると、
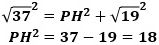
から
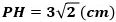
です。
したがって、△DPQの面積は、
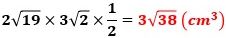
で、これが問1の答えです。
次に問2です。
図4のように、直線DQと直線CPが交わるので、C、D、P、Qは同一平面上にあります。
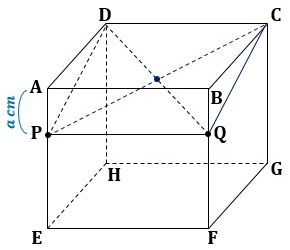
▲図4.C、D、P、Qは同一平面上にあります
このとき、平面ABFEと平面DCGHは平行なので、これらの2平面と平面CDPQの交線PQとDCは平行で、PQ//DCです。
一方、DC//ABからPQ//ABで、さらにAP//BQなので、四角形ABQPは平行四辺形になり、したがってAP=BQ=a(cm)です。
以上から、立体APD-BQCは、底面を△ADP、高さをABとする三角柱なので、その体積は、
6×a×1/2×6= 18a (cm3)で、これが答えです。
最後の問3です。
図5のようにPとF、PとHを結び、その体積を容易に求めることができる、三角錐P-ABD、G-BCD、P-BFG、P-DGH、四角錐P-EFGHを作り、これらの立体を立方体ABCD-EFGHから取り除けば立体G-DPQが残り、その体積を簡単に計算することができます。
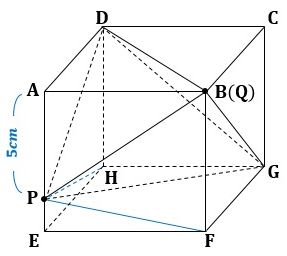
▲図5.立方体を6個の立体に分割します
それでは、各立体の体積を計算しましょう。
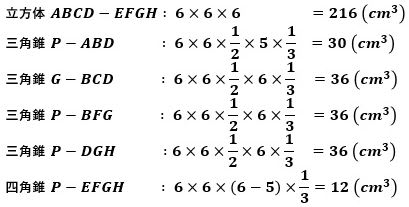
から、立体G-DPQの体積Wは、
W=216-(30+36×3+12)=66(cm3)
です。
このとき、
立体A-DPQは三角錐P-ABDなので、V=30(cm3)で、したがって、V:W=30:66= 5:11 で、これが答えです。
簡単な問題です。
今回は、平成31年度都立日比谷高入試問題を取り上げます。
問題は、
「下の図1に示した立体ABCD-EFGHは1辺の長さが6cmの立方体である。

▲図1.問題図(1)
辺AE上にある点をP、辺BF上にある点をQとする。
頂点Dと点P、点Pと頂点Dをそれぞれ結ぶ。
次の各問に答えよ。
〔問1〕 AP=1cm、BQ=2cmのとき、△DPQの面積は何cm2か。
〔問2〕 頂点Cと点Q、頂点Cと点Pをそれぞれ結んだ場合を考える。
AP=a cm(0<a<6)とする。
直線DQと直線CPが交わるとき、立体APD-BQCの体積をaを用いた式で表せ。
ただし、答えだけではなく、答えを求める過程がわかるように、途中の式や計算なども書け。
〔問3〕 下の図2は、図1において、点Qが頂点Bの位置にあり、頂点Gと頂点D、頂点Gと点P、頂点Gと点Qをそれぞれ結んだ場合を表している。

▲図2.問題図(2)
立体A-DPQの体積をVcm3、立体G-DPQの体積をWcm3とする。
AP=5cmのとき、V:Wを最も簡単な整数の比で表せ。」
です。
△ADPに三平方の定理を適用すると、
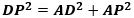
が成り立ち、これにAD=6cm、AP=1cmを代入すると、
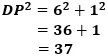
から、図3の左側のように、
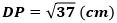
になります。

▲図3.△ADPに三平方の定理を適用しました
また、Pから辺BFに下ろした垂線の足をRとすると、△ADP≡△RPQ(AD=RP、AP=RQ、∠DAP=∠PRQ)になり、したがって、
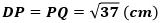
です。
続いて△BDQに三平方の定理を適用すると、
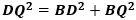
が成り立ち、このときBDは1辺6cmの正方形の対角線なので
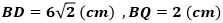
から
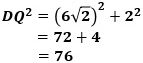
で、したがって、
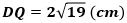
になり、これから△DPQは図3の右側に示すような二等辺三角形になります。
ここで、Pから線分DQに下ろした垂線の足をHとして、△PDHに三平方の定理を適用すると、
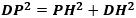
が成り立ち、これに
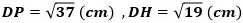
を代入すると、
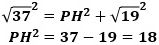
から
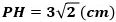
です。
したがって、△DPQの面積は、
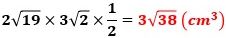
で、これが問1の答えです。
次に問2です。
図4のように、直線DQと直線CPが交わるので、C、D、P、Qは同一平面上にあります。

▲図4.C、D、P、Qは同一平面上にあります
このとき、平面ABFEと平面DCGHは平行なので、これらの2平面と平面CDPQの交線PQとDCは平行で、PQ//DCです。
一方、DC//ABからPQ//ABで、さらにAP//BQなので、四角形ABQPは平行四辺形になり、したがってAP=BQ=a(cm)です。
以上から、立体APD-BQCは、底面を△ADP、高さをABとする三角柱なので、その体積は、
6×a×1/2×6= 18a (cm3)で、これが答えです。
最後の問3です。
図5のようにPとF、PとHを結び、その体積を容易に求めることができる、三角錐P-ABD、G-BCD、P-BFG、P-DGH、四角錐P-EFGHを作り、これらの立体を立方体ABCD-EFGHから取り除けば立体G-DPQが残り、その体積を簡単に計算することができます。

▲図5.立方体を6個の立体に分割します
それでは、各立体の体積を計算しましょう。
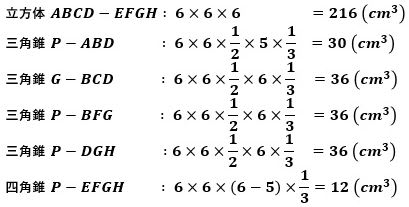
から、立体G-DPQの体積Wは、
W=216-(30+36×3+12)=66(cm3)
です。
このとき、
立体A-DPQは三角錐P-ABDなので、V=30(cm3)で、したがって、V:W=30:66= 5:11 で、これが答えです。
簡単な問題です。




















