役に立つトレミーの定理

こんにちは。東久留米市の学習塾塾長です。

今日、中３の塾生は模擬試験を受けていますが、雨も小雨でよかったです。全員、夏休みに頑張って勉強したので、その成果が現れると思います。

さて今回は図形の問題です。

問題は、
「問題図のように、正五角形ＡＢＣＤＥの外接円の弧ＡＢ上の点をＰとすると、
ＰＡ＋ＰＢ＋ＰＤ＝ＰＣ＋ＰＥ
が成り立つことを示せ。」
です。（シンプルでいいですね）

▲問題図

円に内接する多角形で、線分の長さの関係が問われているので、ここはトレミーの定理を使うのが良さそうです。

トレミーの定理は、以前に取り上げましたが、図１に示したような円に内接する四角形で、辺の長さをａ、ｂ、ｃ、ｄ、対角線の長さをｅ、ｆとすると、
ａｃ＋ｂｄ＝ｅｆ
が成り立つというものです。

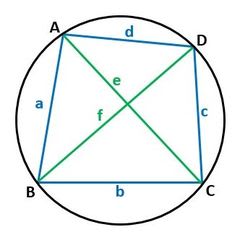
▲図１．トレミーの定理

初めに、正五角形の辺の長さをｐ、対角線の長さをｑとします。

そこで、四角形ＰＡＥＤにトレミーの定理を適用すると、
ＰＡ・ＤＥ＋ＰＤ・ＡＥ＝ＰＥ・ＡＤ
が成り立ち、ＤＥ＝ＡＥ＝ｐ、ＡＤ＝ｑ　から、
ＰＡ・ｐ＋ＰＤ・ｐ＝ＰＥ・ｑ　　　　　　　　　　　　　　　　（１）
です。

同様に、四角形ＰＢＣＤでは、
ＰＢ・ＣＤ＋ＰＤ・ＢＣ＝ＰＣ・ＢＤ
が成り立ち、ＣＤ＝ＢＣ＝ｐ、ＢＤ＝ｑ　から、
ＰＢ・ｐ＋ＰＤ・ｐ＝ＰＣ・ｑ　　　　　　　　　　　　　　　　（２）
です。

さらに、四角形ＰＡＤＢでは、
ＰＡ・ＢＤ＋ＰＢ・ＡＤ＝ＰＤ・ＡＢ
が成り立ち、ＢＤ＝ＡＤ＝ｑ、ＡＢ＝ｐ　から、
ＰＡ・ｑ＋ＰＢ・ｑ＝ＰＤ・ｐ　　　　　　　　　　　　　　　　（３）
です。

最後に、四角形ＰＣＤＥでは、
ＰＣ・ＤＥ＋ＰＥ・ＣＤ＝ＰＤ・ＣＥ
が成り立ち、ＤＥ＝ＣＤ＝ｐ、ＣＥ＝ｑ　から、
ＰＣ・ｐ＋ＰＥ・ｐ＝ＰＤ・ｑ　　　　　　　　　　　　　　　　（４）
です。

これで準備完了です。

導くべき式は、左辺にＰＡ、ＰＢ、ＰＤ、右辺にＰＣ、ＰＥがあるので、（１）から（４）の式も同じように変形します。

ＰＡ・ｐ＋ＰＤ・ｐ　　　　　＝ＰＥ・ｑ　　　　　　　　　　　（１）
ＰＢ・ｐ＋ＰＤ・ｐ　　　　　＝ＰＣ・ｑ　　　　　　　　　　　（２）　　　　　　　　
ＰＡ・ｑ＋ＰＢ・ｑ－ＰＤ・ｐ＝０　　　　　　　　　　　　　（３’）
ＰＤ・ｑ　　　　　　　　　　＝ＰＣ・ｐ＋ＰＥ・ｐ　　　　　　（４’）

これらの（１）（２）（３’）（４’）を辺々足し合わせて、
ＰＡ・ｐ＋ＰＤ・ｐ＋ＰＢ・ｐ＋ＰＤ・ｐ＋ＰＡ・ｑ＋ＰＢ・ｑ－ＰＤ・ｐ＋ＰＤ・ｑ＝ＰＥ・ｑ＋ＰＣ・ｑ＋ＰＣ・ｐ＋ＰＥ・ｐ
とし、これを整理すると、
（ＰＡ＋ＰＢ＋ＰＤ）（ｐ＋ｑ）＝（ＰＣ＋ＰＥ）（ｐ＋ｑ）　　（５）
となります。

ここで、ｐ＋ｑ≠０なので、（５）の両辺をｐ＋ｑで除して、
ＰＡ＋ＰＢ＋ＰＤ＝ＰＣ＋ＰＥ
となり、問題にある式を導くことができました。


トレミーの定理は覚えやすくてパワフルなので、頭に入れておくと役に立ちます。