こんにちは。東久留米市の学習塾塾長です。
予報では最高気温が30°を超えますが、明日はぐっと涼しくなるようです。
先日中1の塾生が円の面積や周の長さに関する問題に取り組んでいました。図1に示したようなもので、1辺aの正方形の右上から左下にかけて囲まれた葉っぱのような図形の面積を求める問題です。(ここで、正方形内の2つの曲線は正方形の左上と右下を中心にして描いた半径aの円の弧です)
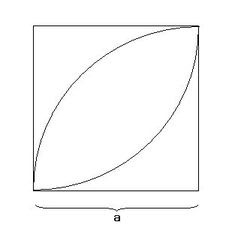
▲図1.円に関する求積問題
この問題は簡単で、1辺aの正方形のなかに、半径aの円の4分の1が2個、つまり半径aの半円があるので、求める面積(葉っぱ形の面積)Sは、
S=a^2π/2-a^2
=a^2(π/2-1) (a^2 はa^2を表します)
正方形の右上から左下に対角線を引いて、4分の1円から三角形を引くことにより求める面積の半分を求め、それを2倍してもOKです。
この円に関する問題は簡単なものですが、次のような難問もあります。それは、「同じ半径をの円を互いに重ならないように平面に並べるとき、最大密度となる配置を求めよ」というものです。
これは、「円の最密充填問題」と言われるもので、1611年に有名な天文学者ケプラーが指摘したのが始まりで、この証明は1831年に大数学者ガウスによって成されました。実は、1773年に大数学者であるラグランジュの数論の二次形式に関する論文のなかに最密充填問題の証明に要するすめての項目が含まれていたのですが、ラグランジュは二次形式と最密充填問題との関連には気付かなかったようです。このように、ケプラー、ラグランジュ、ガウスとスパースターたちが関わった難問です。
そこで今回は、平面上に円を2つの配置方法で敷き詰めたとき、円で覆われる面積の比率を求めたいと思います。
まず、図2のような正方配置の場合です。正方配置は、ある円に対して上下左右に円が接して配置されているものです。
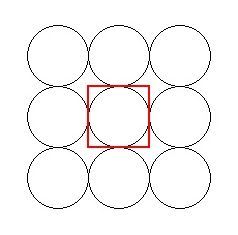
▲図2.円の正方配置
ここで、平面を同じ大きさの正多角形で重なりや隙間がないように敷き詰めることが可能なものは、正三角形、正四角形(正方形)、正六角形であることに注目し、図2の赤線で示した正方形を単位セルとします。すると、円を平面上に無限に敷き詰めたときの円の面積の比率は、単位セルのなかの円の比率と等しいので、それを計算すればOKです。
計算は簡単で、円の半径をrとすると、円の面積S1は、
S1=πr^2
単位セルの面積S0は、
S0=4r^2
したがって、円の面積比率は、
S1/S0=π/4
≒0.758
になります。
次にもう一つの配置である六方配置の場合です。六方配置は図3にあるように、ある円に対して、その周りの6個の円が接していて、周囲の円の中心が正六角形を作る配置です。

▲図3.円の六方配置
正方配置と同様に単位セルを考えますが、六方配置では、図3の赤線で示した正三角形とします。
計算は円の半径をrとすると、円の面積S1’は半円となるので、
S1’=πr^2/2
単位セルの面積S0’は、
S0’=2r・√3r/2
=√3r^2
したがって、円の面積比率は、
S1’/S0’=π/2√3
≒0.907
になります。
六方配置は正方配置に比べて、約1.2倍充填率が大きくなるということなのですが、問題はここからで、六方配置が最も充填率が大きいのか、つまり、もっと充填率が大きい配置方法がないのかという問題に繋がっていきます。
予報では最高気温が30°を超えますが、明日はぐっと涼しくなるようです。
先日中1の塾生が円の面積や周の長さに関する問題に取り組んでいました。図1に示したようなもので、1辺aの正方形の右上から左下にかけて囲まれた葉っぱのような図形の面積を求める問題です。(ここで、正方形内の2つの曲線は正方形の左上と右下を中心にして描いた半径aの円の弧です)

▲図1.円に関する求積問題
この問題は簡単で、1辺aの正方形のなかに、半径aの円の4分の1が2個、つまり半径aの半円があるので、求める面積(葉っぱ形の面積)Sは、
S=a^2π/2-a^2
=a^2(π/2-1) (a^2 はa^2を表します)
正方形の右上から左下に対角線を引いて、4分の1円から三角形を引くことにより求める面積の半分を求め、それを2倍してもOKです。
この円に関する問題は簡単なものですが、次のような難問もあります。それは、「同じ半径をの円を互いに重ならないように平面に並べるとき、最大密度となる配置を求めよ」というものです。
これは、「円の最密充填問題」と言われるもので、1611年に有名な天文学者ケプラーが指摘したのが始まりで、この証明は1831年に大数学者ガウスによって成されました。実は、1773年に大数学者であるラグランジュの数論の二次形式に関する論文のなかに最密充填問題の証明に要するすめての項目が含まれていたのですが、ラグランジュは二次形式と最密充填問題との関連には気付かなかったようです。このように、ケプラー、ラグランジュ、ガウスとスパースターたちが関わった難問です。
そこで今回は、平面上に円を2つの配置方法で敷き詰めたとき、円で覆われる面積の比率を求めたいと思います。
まず、図2のような正方配置の場合です。正方配置は、ある円に対して上下左右に円が接して配置されているものです。

▲図2.円の正方配置
ここで、平面を同じ大きさの正多角形で重なりや隙間がないように敷き詰めることが可能なものは、正三角形、正四角形(正方形)、正六角形であることに注目し、図2の赤線で示した正方形を単位セルとします。すると、円を平面上に無限に敷き詰めたときの円の面積の比率は、単位セルのなかの円の比率と等しいので、それを計算すればOKです。
計算は簡単で、円の半径をrとすると、円の面積S1は、
S1=πr^2
単位セルの面積S0は、
S0=4r^2
したがって、円の面積比率は、
S1/S0=π/4
≒0.758
になります。
次にもう一つの配置である六方配置の場合です。六方配置は図3にあるように、ある円に対して、その周りの6個の円が接していて、周囲の円の中心が正六角形を作る配置です。

▲図3.円の六方配置
正方配置と同様に単位セルを考えますが、六方配置では、図3の赤線で示した正三角形とします。
計算は円の半径をrとすると、円の面積S1’は半円となるので、
S1’=πr^2/2
単位セルの面積S0’は、
S0’=2r・√3r/2
=√3r^2
したがって、円の面積比率は、
S1’/S0’=π/2√3
≒0.907
になります。
六方配置は正方配置に比べて、約1.2倍充填率が大きくなるということなのですが、問題はここからで、六方配置が最も充填率が大きいのか、つまり、もっと充填率が大きい配置方法がないのかという問題に繋がっていきます。




















