こんにちは。東久留米市の学習塾塾長です。
今回は、2011年灘高入試に出題された図形問題を取り上げます。
問題は、
「1辺の長さが1の正十二角形の内部に1辺の長さが1の正三角形16個を下図のように並べた(網掛け部分)。図の5つの頂点を A、B、C、D、E とする。
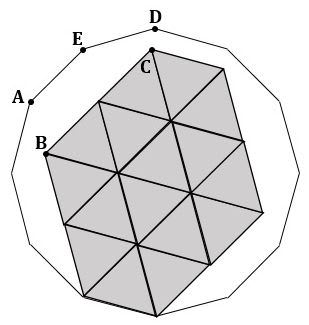
▲問題図
(1) 2点A、B間の距離を求めよ。
(2) 2点C、D間の距離を求めよ。
(3) 五角形ABCDEの面積を求めよ。」
です。
図1のように、Aから反時計回りに正十二角形の頂点をF、G、H、Iとし、さらに内部に図の位置にKをとりましょう。

▲図1.Aから反時計回りに正十二角形の頂点をF、G、H、I、内部にKをとりました
初めに、直線AH上にBがあることと、直線DH上にCがあることを示します。
まず、直線AH上にBがあることを示します。
AH//FGで、正十二角形の外角は30°なので、∠AHG=30°です。
一方、正十二角形の内角が150°から∠GHI=150°で、∠BHI=120°ですから∠BHG=∠GHI-∠BHI=30°です。
したがって、直線AHと直線BHは一致し、直線AH上にBがあることが判りました。
続いて、直線DH上にCがあることを示します。
AF//DH (★)
です。
一方、四角形AHGFは等脚台形なので、∠FAH=30°です。
また、四角形HBCKはひし形で、その対角線は角を二等分するので、∠BHC=∠AHC=∠BHK/2=30°になります。
このとき、∠FAHと∠AHKは直線AFと直線CHの錯角になり、これらが等しいのでAF//CHです。
これと(★)から直線DHと直線CHは一致し、直線DH上にCがあることが判りました。
それでは(1)に取り掛かりましょう。
図3のように、線分AHの長さは、1辺1の正三角形の高さの2つ分の長さと1辺1の正三角形の辺の1つ分の長さの和なので、

です。
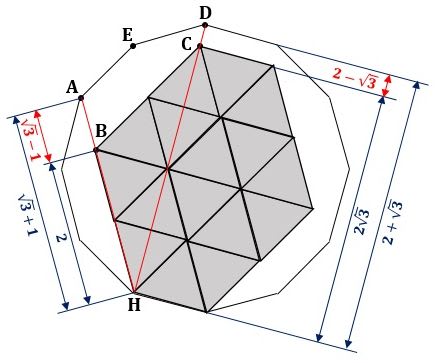
▲図3.2点A、BおよびC、Dの間の距離を計算します
一方、線分BHの長さは、1辺1の正三角形の辺の2つ分の長さなので、
BH=1×2=2
です。
したがって、

から2点A、B間の距離は、

で、これが答えです。
続いて(2)です。
線分DHの長さは、1辺1の正三角形の辺の1/2の2つ分の長さと1辺1の正三角形の高さ2分の長さと1辺1の正三角形の辺の1つ分の長さの和なので、

です。
一方、線分CHの長さは、1辺1の正三角形の高さの4つ分の長さなので、
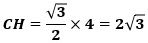
です。
したがって、

から2点C、D間の距離は、

で、これが答えです。
最後の(3)です。
図4のように、五角形ABCDEを台形ABCEと三角形EDCに分割してそれぞれの面積を計算しましょう。
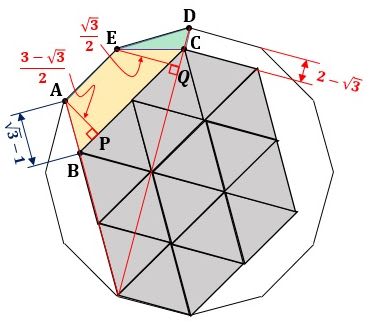
▲図4.五角形ABCDEを台形ABCEと三角形EDCに分割してそれぞれの面積を計算します
ここで、Aから直線BCに下ろした垂線の足をP、Eから直線CDに下ろした垂線の足をQとします。
初めに台形ABCEの面積です。
△ABPは内角が30°、60°、90°の直角三角形なので、

になります。
したがって、台形ABCEの面積は、
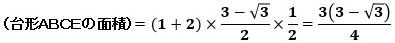
です。
次に△ECDの面積です。
△EDQは内角が30°、60°、90°の直角三角形なので、
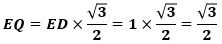
になります。
したがって、△EDCの面積は、
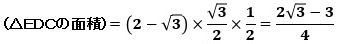
です。
以上から、五角形ABCDEの面積は、

で、これが答えです。
簡単な問題です。
学研CAIスクール 東久留米滝山校
https://caitakiyama.jimdo.com/
TEL 042-472-5533
今回は、2011年灘高入試に出題された図形問題を取り上げます。
問題は、
「1辺の長さが1の正十二角形の内部に1辺の長さが1の正三角形16個を下図のように並べた(網掛け部分)。図の5つの頂点を A、B、C、D、E とする。

▲問題図
(1) 2点A、B間の距離を求めよ。
(2) 2点C、D間の距離を求めよ。
(3) 五角形ABCDEの面積を求めよ。」
です。
図1のように、Aから反時計回りに正十二角形の頂点をF、G、H、Iとし、さらに内部に図の位置にKをとりましょう。

▲図1.Aから反時計回りに正十二角形の頂点をF、G、H、I、内部にKをとりました
初めに、直線AH上にBがあることと、直線DH上にCがあることを示します。
まず、直線AH上にBがあることを示します。
AH//FGで、正十二角形の外角は30°なので、∠AHG=30°です。
一方、正十二角形の内角が150°から∠GHI=150°で、∠BHI=120°ですから∠BHG=∠GHI-∠BHI=30°です。
したがって、直線AHと直線BHは一致し、直線AH上にBがあることが判りました。
続いて、直線DH上にCがあることを示します。
AF//DH (★)
です。
一方、四角形AHGFは等脚台形なので、∠FAH=30°です。
また、四角形HBCKはひし形で、その対角線は角を二等分するので、∠BHC=∠AHC=∠BHK/2=30°になります。
このとき、∠FAHと∠AHKは直線AFと直線CHの錯角になり、これらが等しいのでAF//CHです。
これと(★)から直線DHと直線CHは一致し、直線DH上にCがあることが判りました。
それでは(1)に取り掛かりましょう。
図3のように、線分AHの長さは、1辺1の正三角形の高さの2つ分の長さと1辺1の正三角形の辺の1つ分の長さの和なので、

です。

▲図3.2点A、BおよびC、Dの間の距離を計算します
一方、線分BHの長さは、1辺1の正三角形の辺の2つ分の長さなので、
BH=1×2=2
です。
したがって、

から2点A、B間の距離は、

で、これが答えです。
続いて(2)です。
線分DHの長さは、1辺1の正三角形の辺の1/2の2つ分の長さと1辺1の正三角形の高さ2分の長さと1辺1の正三角形の辺の1つ分の長さの和なので、

です。
一方、線分CHの長さは、1辺1の正三角形の高さの4つ分の長さなので、
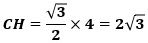
です。
したがって、

から2点C、D間の距離は、

で、これが答えです。
最後の(3)です。
図4のように、五角形ABCDEを台形ABCEと三角形EDCに分割してそれぞれの面積を計算しましょう。

▲図4.五角形ABCDEを台形ABCEと三角形EDCに分割してそれぞれの面積を計算します
ここで、Aから直線BCに下ろした垂線の足をP、Eから直線CDに下ろした垂線の足をQとします。
初めに台形ABCEの面積です。
△ABPは内角が30°、60°、90°の直角三角形なので、

になります。
したがって、台形ABCEの面積は、
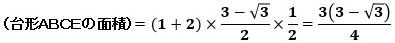
です。
次に△ECDの面積です。
△EDQは内角が30°、60°、90°の直角三角形なので、
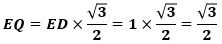
になります。
したがって、△EDCの面積は、
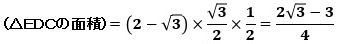
です。
以上から、五角形ABCDEの面積は、

で、これが答えです。
簡単な問題です。
学研CAIスクール 東久留米滝山校
https://caitakiyama.jimdo.com/
TEL 042-472-5533




















※コメント投稿者のブログIDはブログ作成者のみに通知されます