こんにちは。東久留米市の学習塾塾長です。
空には雲が多いものの、それなりの陽射しはあって穏やかな日になりました。明日の気温が少し下がりますが、GW中は今日と同じような天気が続くようです。
さて、今回は2008年日本数学オリンピック予選に出題された最小値を求める問題を取り上げます。
問題は、
「2008個の実数x1、x2、・・・、x2008 があり、lx1l=999であって、2以上2008以下の整数nに対し

が成り立っている。このとき、x1+x2+・・・+x2008 としてありうる最小の値を求めよ。」
です。
早速、取り掛かりましょう。
まず気がつくのが、x1、x2、・・・、x2008 が実数とはいえ、

と

から、x1、x2、・・・、x2008 はすべて整数になります。
次に、xn に絶対値がついていて煩雑なので、

と絶対値を外してしまいましょう。
そこで、

とおき、(3)を使ってTを変形すると、
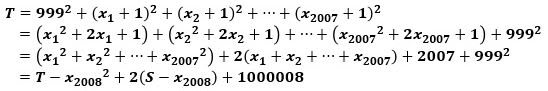
になります。
そして、これを整理して平方完成すると、
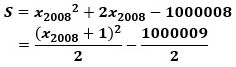
とSの最小値を求めるのに相応しい形になりました。
あとは、

の最小値を求めることになります。
ここで、x2008 が-1 をとることができれば話は簡単ですが、(1)と(2)の制限があるので、それが可能であるか調べる必要があります。
そこで(1)に着目すると、x1 が奇数なので、x2 は偶数、x3 は奇数、・・・と奇数と偶数が順番に繰り返すことが判り、x2008 は偶数です。したがって、残念ながらx2008 は-1になりません。
気を取り直して、(4)を最小にする偶数x2008 を考えましょう。すると、それは0または-2なので、ここではx2008 が0をとることができるかを調べることにします。
1≦n≦999の場合

とすると、x1=-999、lx1l=999で、(2)は成り立ちます。
また、xn<0、xn-1+1≦0から(1)は、

になり、(6)の右辺に(5)を代入すると、

になり、(6)、つまり(1)が成り立ちます。また、x999=-1 になります。
1000≦n≦2008の場合
nが偶数のとき、xn=0
nが奇数のとき、xn=-1
とすると、

かつ、 lx(奇数)l=1、lx(偶数)+1l=1
および、lx(偶数)l=0、lx(奇数)+1l=0
なので、(1)を満たします。
以上から、x1=-999、x2=-998、・・・、x999=-1、x1000=0、x1001=-1、・・・、x2007=-1、x2008=0 は(1)(2)を満たすので、x2008=0は可能で、このとき(x2008+1)^2 の最小値は1 で、Sの最小値は-1000008/2=-500004になります。
したがって、x1+x2+・・・+x2008 としてありうる最小の値は -500004 で、これが答えです。
楽しい問題です。
空には雲が多いものの、それなりの陽射しはあって穏やかな日になりました。明日の気温が少し下がりますが、GW中は今日と同じような天気が続くようです。
さて、今回は2008年日本数学オリンピック予選に出題された最小値を求める問題を取り上げます。
問題は、
「2008個の実数x1、x2、・・・、x2008 があり、lx1l=999であって、2以上2008以下の整数nに対し

が成り立っている。このとき、x1+x2+・・・+x2008 としてありうる最小の値を求めよ。」
です。
早速、取り掛かりましょう。
まず気がつくのが、x1、x2、・・・、x2008 が実数とはいえ、

と

から、x1、x2、・・・、x2008 はすべて整数になります。
次に、xn に絶対値がついていて煩雑なので、

と絶対値を外してしまいましょう。
そこで、

とおき、(3)を使ってTを変形すると、
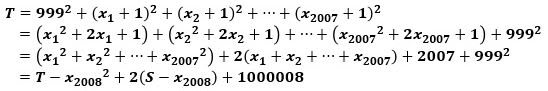
になります。
そして、これを整理して平方完成すると、
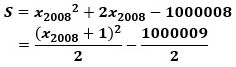
とSの最小値を求めるのに相応しい形になりました。
あとは、

の最小値を求めることになります。
ここで、x2008 が-1 をとることができれば話は簡単ですが、(1)と(2)の制限があるので、それが可能であるか調べる必要があります。
そこで(1)に着目すると、x1 が奇数なので、x2 は偶数、x3 は奇数、・・・と奇数と偶数が順番に繰り返すことが判り、x2008 は偶数です。したがって、残念ながらx2008 は-1になりません。
気を取り直して、(4)を最小にする偶数x2008 を考えましょう。すると、それは0または-2なので、ここではx2008 が0をとることができるかを調べることにします。
1≦n≦999の場合

とすると、x1=-999、lx1l=999で、(2)は成り立ちます。
また、xn<0、xn-1+1≦0から(1)は、

になり、(6)の右辺に(5)を代入すると、

になり、(6)、つまり(1)が成り立ちます。また、x999=-1 になります。
1000≦n≦2008の場合
nが偶数のとき、xn=0
nが奇数のとき、xn=-1
とすると、

かつ、 lx(奇数)l=1、lx(偶数)+1l=1
および、lx(偶数)l=0、lx(奇数)+1l=0
なので、(1)を満たします。
以上から、x1=-999、x2=-998、・・・、x999=-1、x1000=0、x1001=-1、・・・、x2007=-1、x2008=0 は(1)(2)を満たすので、x2008=0は可能で、このとき(x2008+1)^2 の最小値は1 で、Sの最小値は-1000008/2=-500004になります。
したがって、x1+x2+・・・+x2008 としてありうる最小の値は -500004 で、これが答えです。
楽しい問題です。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます