台形の面積の２等分線

こんにちは。東久留米市の学習塾塾長です。

近くの滝山名店会は、ビアガーデンを年に４回開催していて、今日がその１回目なのですが、小雨で気温も２０℃と寒いので大勢の人は集まらないかもしれません。夕方に様子を見に行こうと思います。

台形の面積を２等分する直線を求める問題がありました。三角形の周上の点を通り三角形の面積を２等分する直線や平行四辺形の面積を２等分する直線を求める問題はよく目にしますが、それらに比べて、台形の面積を２等分するものはめずらしいので紹介したいと思います。

平行四辺形の場合、その対角線の交点を通る直線が平行四辺形の面積を２等分します。つまり、対角線の交点でない点Ｐを通り、平行四辺形の面積を２等分する直線は、点Ｐと対角線の交点を通る直線になります。

そこで台形の場合ですが、図１に示すように、上底の中点Ｅと下底の中点Ｆを結んだ線分ＥＦの中点Ｇを求めます。

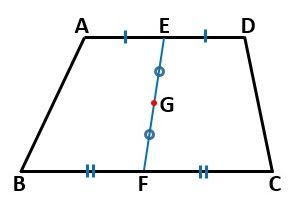
▲図１．上底、下底の中点を結んだ線分ＥＦの中点Ｇを求めます

すると図２のように、点Ｇを通り、かつ、上底、下底と交わる直線Ｌが台形の面積を２等分する直線になります。

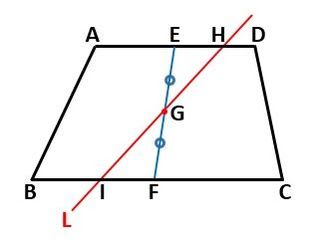
▲図２．点Ｇを通り、上底、下底と交わる台形面積の２等分線Ｌ

証明は、
台形の面積＝（上底＋下底）×高さ÷２　
と
△ＧＥＨ≡△ＧＦＩから導き出される、ＥＨ＝ＦＩ
を使えば簡単です。

台形ＡＢＩＨの面積をＳとすると、
Ｓ＝（ＡＨ＋ＢＩ）×高さ÷２
　＝（ＡＥ＋ＥＨ＋ＢＦ－ＦＩ）×高さ÷２
で、ＥＨ＝ＦＩから
Ｓ＝（ＡＥ＋ＢＦ）×高さ÷２
です。

同様に、台形ＣＤＨＩの面積をＴとすると、
Ｔ＝（ＤＨ＋ＣＩ）×高さ÷２
　＝（ＤＥ－ＥＨ＋ＣＦ＋ＦＩ）×高さ÷２
　＝（ＤＥ＋ＣＦ）×高さ÷２
です。

ここで、ＡＥ＝ＤＥ、ＢＦ＝ＣＦから
Ｓ＝Ｔ
となります。

このように、点Ｇを通る直線で、上底および下底と交わるものは台形の面積を２等分するのですが、上底と下底の少なくとも一方と交わらない直線は台形の面積の２等分線にならないので注意しましょう。

例えば図３のように、点Ｇを通り、上底、下底と平行な直線は、台形の面積の２等分線にならないのは明らかです。（図３の場合、台形ＡＨＩＤの面積＜台形ＨＢＣＩの面積　です）

▲図３．点Ｇを通り、上底、下底と交わらない直線Ｌの場合

あまり使うことはないかもしれませんが、頭に入れておくと役に立つこともあるかもしれません。