切断三角柱の体積の求め方

こんにちは。東久留米市の学習塾塾長です。

早実と東海大甲府の試合は、早実が勝ちました。清宮選手は本塁打など大当たりで、一方、東海大甲府も素晴らしい守備で粘りましたが、一歩及びませんでした。どちらのチームも強くいい試合でした。

先日、切断三角柱（断頭三角柱）の体積を求める問題を取り上げましたが、その公式の説明を端折ったので、今回はそれについて調べていきます。

前回使った公式は、図のような切断三角柱ＡＢＣ－ＤＥＦで、△ＡＢＣ＝Ｓ、ＡＤ＝ａ、ＢＥ＝ｂ、ＣＦ＝ｃ、ａ≧ｂ≧ｃとすると、切断三角柱ＡＢＣ－ＤＥＦの体積Ｖは、
Ｖ＝Ｓ×（ａ＋ｂ＋ｃ）/３　　　　　　　　　　　　　　　　　（１）
というものです。

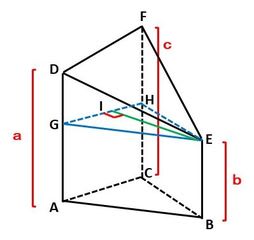
▲図．切断三角柱ＡＢＣ－ＤＥＦ

まず、三角柱ＡＢＣ－ＤＥＦを、△ＡＢＣに平行な△ＧＥＨで，三角柱ＡＢＣ－ＧＥＨと四角錐Ｅ－ＤＧＨＦの２個の立体に分割します。

すると、下部にある三角柱ＡＢＣ－ＧＥＨの体積Ｖ1は、
Ｖ1＝Ｓ×ｂ　　　　　　　　　　　　　　　　　　　　　　　　（２）
になります。

次に、上部にある四角錐Ｅ－ＤＧＨＦの体積Ｖ2は、ＥからＧＨに下ろした垂線の足をＩとすると、
Ｖ2＝（台形ＤＧＨＦの面積）×ＥＩ×１/３　　　　　　　　　　（３）
になります。

ここで、台形ＤＧＨＦの面積は、
（台形ＤＧＨＦの面積）＝（ＤＧ＋ＦＨ）×ＧＨ×１/２
　　　　　　　　　　　＝（ａ－ｂ＋ｃ－ｂ）×ＧＨ×１/２
　　　　　　　　　　　＝（ａ－２ｂ＋ｃ）×ＧＨ×１/２　　　　（４）
で、（４）を（３）に代入して、
Ｖ2＝（台形ＤＧＨＦの面積）×ＥＩ×１/３
　　＝（ａ－２ｂ＋ｃ）×ＧＨ×１/２×ＥＩ×１/３
　　＝（ａ－２ｂ＋ｃ）×ＧＨ×ＥＩ×１/６　　　　　　　　　　（５）
です。

一方、△ＧＥＨの面積＝△ＡＢＣの面積＝Ｓなので、
Ｓ＝ＧＨ×ＥＩ×１/２
で、これを変形して、
ＧＨ×ＥＩ＝２×Ｓ
とします。　　　　　　　　　　　　　　　　　　　　　　　　（６）

そして、（６）を（５）に代入して、
Ｖ2＝（ａ－２ｂ＋ｃ）×２×Ｓ×１/６
　　＝（ａ－２ｂ＋ｃ）×Ｓ×１/３　　　　　　　　　　　　　　（７）
となります。

最後に、切断三角柱ＡＢＣ－ＤＥＦの体積Ｖは、（２）（７）から、
Ｖ＝Ｖ1＋Ｖ2
　＝Ｓ×ｂ＋（ａ－２ｂ＋ｃ）×Ｓ×１/３
　＝Ｓ×（ａ＋ｂ＋ｃ）/３
と（１）を導くことができました。


三角柱の両端が切断された切断三角柱の体積を求めるときは、上記の操作を２回繰り返すことで求めることができます。