こんにちは。東久留米市の学習塾塾長です。
今日も朝から快晴で予想最高気温は29℃と暑い日になりそうです。明日からは前線を伴った低気圧の影響で天気は下り坂で、明日、明後日は曇り、雨の空模様です。
さて、今回は2004年ジュニア数学オリンピック予選に出題された数の問題を取り上げます。
問題は、
「
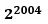
を

で割ってそれぞれの商と余りを求める。このとき、商として現われる整数は何種類あるか。」
です。
早速、取り掛かりましょう。
整数Nを√N以下の整数で割ったときの商はとびとびの整数になり、一方、√Nより大きいの整数で割ったときの商は連続した整数になります。
例えば、N=10とすると、√N=3.16・・・で、10を3.16・・・以下の整数1、2、3で割ったときの商は、10、5、3と飛び飛びの整数になり、3.16・・・より大きい整数4、5、6、7、8、9、10で割ったときの商は、2、1と連続した整数になります。
そこで、2^2004 を、1以上2^1002 以下の整数で割ったときの商と、2^1002+1以上2^2004 以下の整数で割ったときの商に分けて調べることにしましょう。
●2^2004 を1以上2^1002 以下の整数で割る場合
1≦A≦2^1002 (Aは整数)として、2^2004 を連続した2つの整数A-1とAで割ったときの差を考えると、
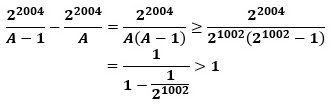
が成り立ちます。
つまり、2^2004 を連続する2つの整数で割ったときの商の差は1より大きいので、すべての商の整数部分は相異なる整数になります。
したがって、商として現われる整数の種類は、整数Aの個数に等しく、それは2^1002 (種類)です。
●2^2004 を2^1002+1以上2^2004以下の整数で割る場合
2^1002+1≦B≦2^2004 (Bは整数)とすると、2^2004 をBで割ったときの商2^2004/Bは、
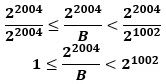
で、さらに、
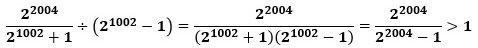
から、2^2004/Bは2^1002-1より大きい値を取り得るので、2^2004/Bの整数部分は1以上2^1002-1以下の整数になります。 (★)
一方、2^2004 を連続する2つの整数B-1とBで割ったときの商の差を考えると、
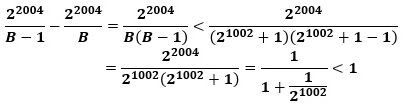
が成り立ちます。
つまり、(★)と、2^2004 を連続する2つの整数で割ったときの商の差は1より小さいことから、2^2004/Bの整数部分は1以上2^1002-1以下のすべての整数をとることになります。
したがって、商として現われる整数の種類は、2^1002-1 (種類)です。
以上から、
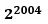
を

で割ったときの商に現われる整数の種類は、
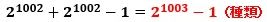
で、これが答えです。
楽しい問題です。
今日も朝から快晴で予想最高気温は29℃と暑い日になりそうです。明日からは前線を伴った低気圧の影響で天気は下り坂で、明日、明後日は曇り、雨の空模様です。
さて、今回は2004年ジュニア数学オリンピック予選に出題された数の問題を取り上げます。
問題は、
「
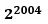
を

で割ってそれぞれの商と余りを求める。このとき、商として現われる整数は何種類あるか。」
です。
早速、取り掛かりましょう。
整数Nを√N以下の整数で割ったときの商はとびとびの整数になり、一方、√Nより大きいの整数で割ったときの商は連続した整数になります。
例えば、N=10とすると、√N=3.16・・・で、10を3.16・・・以下の整数1、2、3で割ったときの商は、10、5、3と飛び飛びの整数になり、3.16・・・より大きい整数4、5、6、7、8、9、10で割ったときの商は、2、1と連続した整数になります。
そこで、2^2004 を、1以上2^1002 以下の整数で割ったときの商と、2^1002+1以上2^2004 以下の整数で割ったときの商に分けて調べることにしましょう。
●2^2004 を1以上2^1002 以下の整数で割る場合
1≦A≦2^1002 (Aは整数)として、2^2004 を連続した2つの整数A-1とAで割ったときの差を考えると、
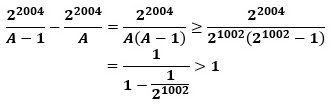
が成り立ちます。
つまり、2^2004 を連続する2つの整数で割ったときの商の差は1より大きいので、すべての商の整数部分は相異なる整数になります。
したがって、商として現われる整数の種類は、整数Aの個数に等しく、それは2^1002 (種類)です。
●2^2004 を2^1002+1以上2^2004以下の整数で割る場合
2^1002+1≦B≦2^2004 (Bは整数)とすると、2^2004 をBで割ったときの商2^2004/Bは、
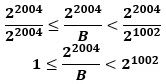
で、さらに、
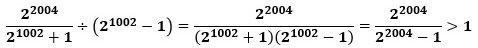
から、2^2004/Bは2^1002-1より大きい値を取り得るので、2^2004/Bの整数部分は1以上2^1002-1以下の整数になります。 (★)
一方、2^2004 を連続する2つの整数B-1とBで割ったときの商の差を考えると、
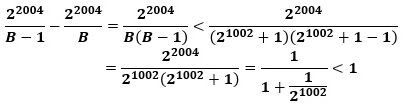
が成り立ちます。
つまり、(★)と、2^2004 を連続する2つの整数で割ったときの商の差は1より小さいことから、2^2004/Bの整数部分は1以上2^1002-1以下のすべての整数をとることになります。
したがって、商として現われる整数の種類は、2^1002-1 (種類)です。
以上から、
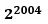
を

で割ったときの商に現われる整数の種類は、
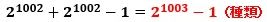
で、これが答えです。
楽しい問題です。










