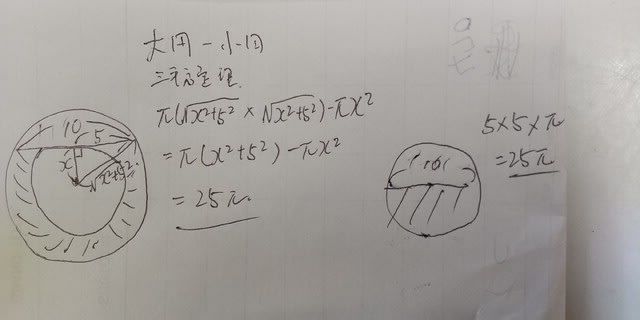
「やっぱり主観とかじゃなくて、データや数値に基づくエピデンスを示してくれきゃ話になんないよね。」とお客様。
そのご意見に異議がある訳ではないんですが、プロや専門家間ならともかく、僕ら一般人や前のめり型だと自覚がある方は、数値やグラフ、データのみ根拠にした結論というものに対し、注意が必要かと。
穴と1箇所接点を持つ外周を結んだ直線が10㎝であるドーナツ型平面図(題図左)。三平方の定理からその面積を計算すれば25π㎠。一方穴のない直径10㎝のドーナツ平面積(題図右)も、また25π㎠になります。でも、だから同じとはならないでしょう。
そこには穴の有無という、質的定性的な大きな差異がある。
そんなの解ってるよと、おっしゃる向きも多いかと存じますが。
・・・ご自分やお子さんのテストの答案用紙が返されてきた時、点数だけ見ていた方はいらっしゃらないでしょうか?
そいう教育、環境下だったせいか、一般的に順位や数値、グラフ化されると、そこに絶対的な真実を見てしまいがちな国民性を感じることがあります。解りやすいことも有り、切り取られたエビデンスが独り歩きしてしまうこともある。
ですから全体をご存じでも、その数値という重力に、無意識に引っ張られている可能性がある自覚を持つのが肝要かと。
何事もバランスだと思います。
そのご意見に異議がある訳ではないんですが、プロや専門家間ならともかく、僕ら一般人や前のめり型だと自覚がある方は、数値やグラフ、データのみ根拠にした結論というものに対し、注意が必要かと。
穴と1箇所接点を持つ外周を結んだ直線が10㎝であるドーナツ型平面図(題図左)。三平方の定理からその面積を計算すれば25π㎠。一方穴のない直径10㎝のドーナツ平面積(題図右)も、また25π㎠になります。でも、だから同じとはならないでしょう。
そこには穴の有無という、質的定性的な大きな差異がある。
そんなの解ってるよと、おっしゃる向きも多いかと存じますが。
・・・ご自分やお子さんのテストの答案用紙が返されてきた時、点数だけ見ていた方はいらっしゃらないでしょうか?
そいう教育、環境下だったせいか、一般的に順位や数値、グラフ化されると、そこに絶対的な真実を見てしまいがちな国民性を感じることがあります。解りやすいことも有り、切り取られたエビデンスが独り歩きしてしまうこともある。
ですから全体をご存じでも、その数値という重力に、無意識に引っ張られている可能性がある自覚を持つのが肝要かと。
何事もバランスだと思います。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます