三角形の面積の３等分

こんにちは。東久留米市の学習塾塾長です。

先週に比べて気温が下がって少し過ごしやすくなりましたが、蒸し暑い日が続きます。

さて、今回は三角形の面積の３等分についてです。三角形の面積を３等分する方法はいろいろありますが、図１のように一つの頂点と底辺を３等分した点とを結ぶと、△ＡＢＰ＝△ＡＰＱ＝△ＡＱＣ　となり、△ＡＢＣの面積を３等分することができます。

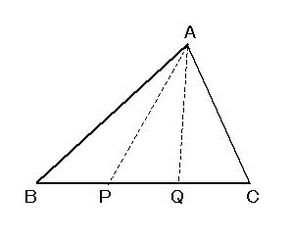
▲図１．三角形の面積の３等分（底辺を３等分）

また、図２のように三角形の重心も△ＧＡＢ＝△ＧＢＣ＝△ＧＣＡ　と△ＡＢＣの面積を３等分することができます。

▲図２．三角形の面積の３等分（重心を利用）

その他に相似を利用する方法があります。例えば、相似比が１：√２：√３　の場合、面積比は相似比の２乗になるので、それは、１：２：３　となます。つまり、元の三角形の１辺を１：√２：√３　に分けて相似三角形を作ってできる３つの領域は、それぞれの面積が等しすく、すなわち、元の三角形の面積を３等分することができます。

ここで問題となるのが、１：√２：√３　の作図ですが、これは簡単で図３のような三角定規の辺の長さが√２、√３を与えてくれます。

▲図３．√２と√３の作図

これらの長さの線分を作図して図４のように三角形の１辺を１：√２：√３　に内分した点から対辺に平行線を引けば元の三角形の面積を３等分することができます。

▲図４．三角形の面積の３等分（√２、√３を利用）

さらに、ｙ＝ｘ^2　の放物線を使う方法もあります。ｙ＝ｘ^2　は相似比をｘとしたときの面積比を表すので、図５のようにｙ＝１、２および３に対応するｘの値が、それぞれ、１、√２および√３となり、図のように△ＡＢＣを３等分することができます。但し、放物線はコンパスと定規だけでは作図できないのが難点ですが。

▲図５．三角形の面積の３等分（放物線を利用）

他にも面白い三角形の面積の３等分方法があるかもしれません。見つけたら是非教えてください。次回は角の３等分を取り上げます。