こんにちは。東久留米市の学習塾塾長です。
今回は、整数問題です。
問題は、
「 n進法表示で 11111(n) となる数が平方数になるような2以上の整数 n をすべて求めよ。」
です。
11111(n) を十進法に直すと、

です。
ここから、連続する2つの整数N、N+1の平方数

と
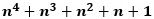
との大小関係を調べていきます。
● nが偶数の場合

とすると、
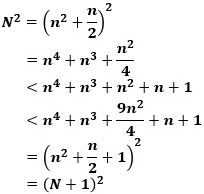
から

で、
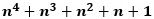
は、平方数になりません。
● nが奇数の場合

とすると、

と

から

です。
ここで、
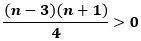
のとき、つまり、n>3のとき、

から

は平方数になりません。
また、

のとき、つまり、n=3のとき、
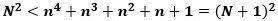
から

になり、

は平方数になります。
実際に、

と、11111(3) は平方数です。
以上から、11111(n) が平方数となる整数 n は 3 で、これが答えです。
簡単な問題です。
今回は、整数問題です。
問題は、
「 n進法表示で 11111(n) となる数が平方数になるような2以上の整数 n をすべて求めよ。」
です。
11111(n) を十進法に直すと、

です。
ここから、連続する2つの整数N、N+1の平方数

と
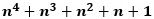
との大小関係を調べていきます。
● nが偶数の場合

とすると、
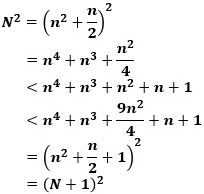
から

で、
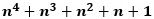
は、平方数になりません。
● nが奇数の場合

とすると、

と

から

です。
ここで、
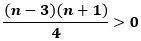
のとき、つまり、n>3のとき、

から

は平方数になりません。
また、

のとき、つまり、n=3のとき、
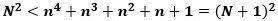
から

になり、

は平方数になります。
実際に、

と、11111(3) は平方数です。
以上から、11111(n) が平方数となる整数 n は 3 で、これが答えです。
簡単な問題です。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます