こんにちは。東久留米市の学習塾塾長です。
今回は、令和2年度都立国立高の問題です。
問題は、
「下の図のように、3つの袋A、B、Cがあり、
袋Aの中には、1、2、3の数字が1つずつ書かれた3個の玉が、
袋Bの中には、1、2、3、4の数字が1つずつ書かれた4個の玉が、
袋Cの中には、1、2、3、4、5の数字が1つずつ書かれた5個の玉が
入っている。

3つの袋A、B、Cから同時に玉をそれぞれ1つずつ取り出す。
このとき、取り出した3つの玉に書かれた数の和が7になる確率を求めよ。
ただし、3つの袋それぞれにおいて、どの玉が取り出されることも同様に確からしいものとする。」
です。
3つの袋から取り出した玉に書かれた数の和が7になる組合せをどのように調べても難しくありませんが、ここでは、袋Aから取り出した玉に書かれた数で場合分けして勘定することにしましょう。
● 袋Aの玉に書かれた数が1の場合
袋B、Cから取り出された玉に書かれた数の和が6になる組合せ(袋Bの数,袋Cの数)は、
(1,5)、(2,4)、(3,3)、(4,2)
の4通りです。
● 袋Aの玉に書かれた数が2の場合
袋B、Cから取り出された玉に書かれた数の和が5になる組合せ(袋Bの数,袋Cの数)は、
(1,4)、(2,3)、(3,2)、(4,1)
の4通りです。
● 袋Aの玉に書かれた数が3の場合
袋B、Cから取り出された玉に書かれた数の和が4になる組合せ(袋Bの数,袋Cの数)は、
(1,3)、(2,2)、(3,1)
の3通りです。
したがって、3つの袋から取り出した3つの玉に書かれた数の和が7になる組合せは、4+4+3=11(通り)です。
このとき、それぞれの袋から1つずつ玉を取り出す場合の数は、3×4×5=60(通り)であることから、求める確率は、
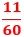
で、これが答えです。
簡単な問題です。
今回は、令和2年度都立国立高の問題です。
問題は、
「下の図のように、3つの袋A、B、Cがあり、
袋Aの中には、1、2、3の数字が1つずつ書かれた3個の玉が、
袋Bの中には、1、2、3、4の数字が1つずつ書かれた4個の玉が、
袋Cの中には、1、2、3、4、5の数字が1つずつ書かれた5個の玉が
入っている。

3つの袋A、B、Cから同時に玉をそれぞれ1つずつ取り出す。
このとき、取り出した3つの玉に書かれた数の和が7になる確率を求めよ。
ただし、3つの袋それぞれにおいて、どの玉が取り出されることも同様に確からしいものとする。」
です。
3つの袋から取り出した玉に書かれた数の和が7になる組合せをどのように調べても難しくありませんが、ここでは、袋Aから取り出した玉に書かれた数で場合分けして勘定することにしましょう。
● 袋Aの玉に書かれた数が1の場合
袋B、Cから取り出された玉に書かれた数の和が6になる組合せ(袋Bの数,袋Cの数)は、
(1,5)、(2,4)、(3,3)、(4,2)
の4通りです。
● 袋Aの玉に書かれた数が2の場合
袋B、Cから取り出された玉に書かれた数の和が5になる組合せ(袋Bの数,袋Cの数)は、
(1,4)、(2,3)、(3,2)、(4,1)
の4通りです。
● 袋Aの玉に書かれた数が3の場合
袋B、Cから取り出された玉に書かれた数の和が4になる組合せ(袋Bの数,袋Cの数)は、
(1,3)、(2,2)、(3,1)
の3通りです。
したがって、3つの袋から取り出した3つの玉に書かれた数の和が7になる組合せは、4+4+3=11(通り)です。
このとき、それぞれの袋から1つずつ玉を取り出す場合の数は、3×4×5=60(通り)であることから、求める確率は、
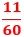
で、これが答えです。
簡単な問題です。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます