円についての基本定理

こんにちは。東久留米市の学習塾塾長です。

いくつかの天気予報での降水確率は６０～９０％となっていますが、天気図を見ると梅雨前線が南に下がっているので、このまま曇りの天気が続くといいですね。いずれにしても、明日は晴れるようです。

中３数学では円について勉強します。円に関連する定理はたくさんあるのですが、「日日のハイレベル演習」に挙げられているのが、
（１）円周角の定理
（２）内接四角形の性質
（３）アルハゼンの定理
（４）方べきの定理
（５）接弦定理
（６）トレミーの定理
です。（１）～（３）が基本的な諸定理、（４）～（６）が発展的な諸定理に分類してあるので、少なくとも（１）～（３）はマスターしておくのが良いでしょう。（ただし、（３）のアルハゼンの定理は、手元にある「モノグラフ公式集」にはありませんでした）

まず（１）の円周角の定理は、教科書にたくさんのページが割かれている最も重要なもので、図１のように、円Ｏの決まった弧ＡＢに対する円周角（∠ＡＰＢ、∠ＡＱＢ）はすべて等しく、弧ＡＢに対する中心角∠ＡＯＢの１/２である（∠ＡＰＢ＝１/２∠ＡＯＢ）、というものです。

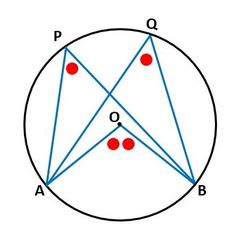
▲図１．円周角の定理

（２）の内接四角形の性質は、図２のように、円に内接する四角形ＡＢＣＤにおいて、２組の対角の和（∠Ａ＋∠Ｃ、∠Ｂ＋∠Ｄ）はそれぞれ１８０°である、というものです。

▲図２．内接四角形の性質

（３）のアルハゼンの定理は、図３のように、直線ＡＥと直線ＢＥがそれぞれ円と２点で交わっているとき、円内の角（∠ＡＦＢ）は、弧ＡＢと弧ＣＤの円周角の和であり、円外の角（∠ＡＥＢ）は、弧ＡＢと弧ＣＤの円周角の差である、というものです。

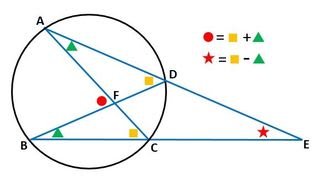
▲図３．アルハゼンの定理

（１）は次のように証明することができます。

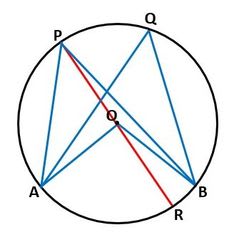
▲図４．円周角の定理の証明

図４のように、Ｐと円の中心Ｏを結んだ直線と円Ｏとの交点をＲとすると、△ＯＡＰと△ＯＢＰは二等辺三角形になり、それぞれの底角の和は、∠ＡＯＲおよび∠ＲＯＢになるので、
∠ＡＯＢ＝∠ＡＯＲ＋∠ＲＯＢ
　　　　＝２∠ＡＰＯ＋２∠ＢＰＯ
　　　　＝２（∠ＡＰＯ＋∠ＢＰＯ）
　　　　＝２∠ＡＰＢ
です。

したがって、中心角は円周角の２倍になります。

さらに、同じ中心角に対する円周角は等しくなるので、決まった弧に対する円周角は等しくなります。

続いて（２）の証明です。

図５のように、円の中心ＯとＢ、Ｄを結びます。円周角の定理から、∠Ａ＝１/２∠ＢＯＤ（弧ＢＣＤに対する中心角）、∠Ｃ＝１/２∠ＤＯＢ（弧ＤＡＢに対する中心角）なので、
∠Ａ＋∠Ｃ＝１/２∠ＢＯＤ（弧ＢＣＤに対する中心角）＋１/２∠ＤＯＢ（弧ＤＡＢに対する中心角）
　　　　　＝１/２（∠ＢＯＤ＋∠ＤＯＢ）
　　　　　＝１/２×３６０°
　　　　　＝１８０°
となります。　　　　　

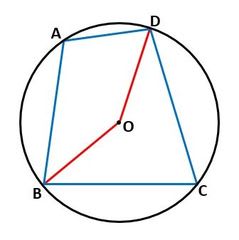
▲図５．内接四角形の性質

最後に（３）ですが、図３で、∠ＡＦＢは、△ＡＤＦ（△ＢＣＦ）の外角なので、
∠ＡＦＢ＝∠ＦＡＤ＋∠ＦＤＡ
　　　　＝∠ＦＢＣ＋∠ＦＣＢ
となり、∠ＡＣＢと∠ＡＤＢは、それぞれ△ＡＣＥおよび△ＢＤＥの外角なので、
∠ＡＣＢ＝∠ＣＡＥ＋∠ＣＥＡ、
∠ＡＤＢ＝∠ＤＢＣ＋∠ＢＥＤ
より、
∠ＣＥＡ＝∠ＡＣＢ－∠ＣＡＥ
∠ＢＥＤ＝∠ＡＤＢ－∠ＤＢＣ
であることが判ります。


（３）のアルハゼンの定理は円周角と三角形の外角で導くことができるので、覚えておく必要はないですが、円周角の定理と内接四角形の性質は頻出なので頭にいれておくと良いでしょう。残りの発展的な諸定理（４）（５）（６）については、またの機会に取り上げます。