こんにちは。東久留米市の学習塾塾長です。
昨夜は息子と夕食(ほとんど飲んでいましたが)に出てしまったので、楽しみにしているNHK大河ドラマ「花燃ゆ」を観ることができませんでした。録画してあるので早めに観たいと思います。出足から低視聴率で第2回放送でもさらに下がりましたが、昨夜の第3回放送では少し持ち直したようで良かったです。
さて、今回は平成24年度東大大学院工学系研究科システム創成学の入試問題です。
問題は、
「最初、テーブルの上にトランプのカード52枚が全て裏向けにして一列に並べられていた。1人目がやってきて、全てのカードを表にして行った。2人目がやってきて、左から偶数枚目のカードを全てひっくり返して行った。3人目がやってきて、左から3枚目、6枚目、9枚目、・・・と3枚おきにカードをひっくり返して行った。N人目がやってきて、左からN枚目ごとのカードをひっくり返して行った。最後に52人目がやってきて、右端のカードをひっくり返して行った。52人目が行ってしまった後、表を向いているカードは何枚あるか。」
です。
算数、数学の問題を解く上で図表を描いてみることは大切です。そこで次の表を作りました。
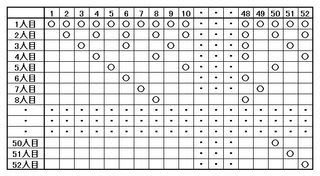
▲問題の操作を表にしました
この表から52名の人が自分の順番の倍数となるカードをひっくり返して行くことが判ります。
そして、あるカードが何回ひっくり返されたかでそのカードの最終的な表裏が決まりますが、初めは全て裏向けだったので、奇数回ひっくり返されたカードが表向きになることが判ります。
つまり、1から52までの自然数について、約数の個数が奇数個持つものがいくつあるかを調べればよいことが判ります。
ここまでくればあとは簡単で、1から52までの自然数の約数を数え上げてもOKですし、少しい工夫するのも良いでしょう。
但し、カードが1000枚とか多い場合には数え上げるのは一仕事なので、ここでは少し工夫して調べていきましょう。
まず、自然数と約数の個数の関係を思い出しましょう。
ある自然数nを素因数分解して、
n=a^p・b^q・・・c^r
と表すと、nの約数の個数mは、
m=(p+1)(q+1)・・・(r+1)
になります。
ここで、もしp、q、・・・、rが全て偶数であれば、p+1、q+1、・・・、r+1は全て奇数になるので、mは奇数になります。(もし、p、q、・・・、rのいずれか一つでも奇数であれば、mは偶数になります)
これを手掛かりにして調べていきます。
n(1≦n≦52、nは自然数)を素因数分解して、
n=a^p・b^q・・・c^r (1)
と表すことができるとすると、
p、q、・・・、rが全て偶数のとき、nの約数は奇数個となります。
そこで、p=2p'、q=2q'、・・・、r=2r' (p'、q'、・・・、r'は自然数)
とおき、(1)に代入すると、
n=a^2p'・b^2q'・・・c^2r'
=(a^p'・b^q’・・・c^r')^2
となり、これはnが平方数であることを表します。
したがって、1から52までの自然数のうち、平方数であるものの個数を調べればOKで、それは、1、4、9、16、25、36、49の7個ですから、答えは7枚になります。
繰り返しになりますが、算数、数学の問題を解くときは、図表を使って考えることが大切なので、面倒臭がらず図表を描く習慣を身につけましょう。
昨夜は息子と夕食(ほとんど飲んでいましたが)に出てしまったので、楽しみにしているNHK大河ドラマ「花燃ゆ」を観ることができませんでした。録画してあるので早めに観たいと思います。出足から低視聴率で第2回放送でもさらに下がりましたが、昨夜の第3回放送では少し持ち直したようで良かったです。
さて、今回は平成24年度東大大学院工学系研究科システム創成学の入試問題です。
問題は、
「最初、テーブルの上にトランプのカード52枚が全て裏向けにして一列に並べられていた。1人目がやってきて、全てのカードを表にして行った。2人目がやってきて、左から偶数枚目のカードを全てひっくり返して行った。3人目がやってきて、左から3枚目、6枚目、9枚目、・・・と3枚おきにカードをひっくり返して行った。N人目がやってきて、左からN枚目ごとのカードをひっくり返して行った。最後に52人目がやってきて、右端のカードをひっくり返して行った。52人目が行ってしまった後、表を向いているカードは何枚あるか。」
です。
算数、数学の問題を解く上で図表を描いてみることは大切です。そこで次の表を作りました。

▲問題の操作を表にしました
この表から52名の人が自分の順番の倍数となるカードをひっくり返して行くことが判ります。
そして、あるカードが何回ひっくり返されたかでそのカードの最終的な表裏が決まりますが、初めは全て裏向けだったので、奇数回ひっくり返されたカードが表向きになることが判ります。
つまり、1から52までの自然数について、約数の個数が奇数個持つものがいくつあるかを調べればよいことが判ります。
ここまでくればあとは簡単で、1から52までの自然数の約数を数え上げてもOKですし、少しい工夫するのも良いでしょう。
但し、カードが1000枚とか多い場合には数え上げるのは一仕事なので、ここでは少し工夫して調べていきましょう。
まず、自然数と約数の個数の関係を思い出しましょう。
ある自然数nを素因数分解して、
n=a^p・b^q・・・c^r
と表すと、nの約数の個数mは、
m=(p+1)(q+1)・・・(r+1)
になります。
ここで、もしp、q、・・・、rが全て偶数であれば、p+1、q+1、・・・、r+1は全て奇数になるので、mは奇数になります。(もし、p、q、・・・、rのいずれか一つでも奇数であれば、mは偶数になります)
これを手掛かりにして調べていきます。
n(1≦n≦52、nは自然数)を素因数分解して、
n=a^p・b^q・・・c^r (1)
と表すことができるとすると、
p、q、・・・、rが全て偶数のとき、nの約数は奇数個となります。
そこで、p=2p'、q=2q'、・・・、r=2r' (p'、q'、・・・、r'は自然数)
とおき、(1)に代入すると、
n=a^2p'・b^2q'・・・c^2r'
=(a^p'・b^q’・・・c^r')^2
となり、これはnが平方数であることを表します。
したがって、1から52までの自然数のうち、平方数であるものの個数を調べればOKで、それは、1、4、9、16、25、36、49の7個ですから、答えは7枚になります。
繰り返しになりますが、算数、数学の問題を解くときは、図表を使って考えることが大切なので、面倒臭がらず図表を描く習慣を身につけましょう。










