中学生でも解ける東大大学院入試問題（８７）

こんにちは。東久留米市の学習塾塾長です。

昨日に続いて冬晴れの良い天気になりました。明日は雨で気温も上がらず寒くなるようですが、明後日からは少し暖かくなるようです。

さて、今回は平成２４年度東大大学院新領域創成科学研究科海洋技術環境学の入試問題です。

問題は、
「Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆの６名が円形のテーブルに座る。テーブルは６等分されていて、テーブルの真ん中に回転する円盤が置かれている。この円盤も矢印で６等分されていて、矢印の各方向に０から５までの数字が下の図のように書かれている。円盤を回して、止まったときの各方向の数字が自分の点になる。これを５回繰り返し、合計点で最高点であった者を勝ちとする。図は１回目を回し終えたときの様子で、Ｃが５点を取ってリードしている。続いて２回目の後でＤ一人がリードし、５回目が終わった時Ａ一人が勝った。各競技者の最終得点はそれぞれ何点か？」

▲問題図

この問題のポイントは、各人の座っている位置と矢印の数字の位置が変わらないということです。例えば、１点取った人の向かい側の人は４点取るということで、この関係を利用して最終的にＡが一人勝つ条件を調べれば解けそうです。そこで、その関係を表１にまとめておきましょう。

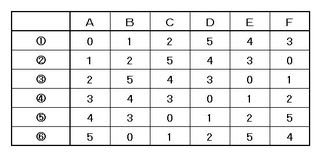
▲表１．各人が取り得る得点の関係

それでは１、２回目の試行結果を調べていきましょう。

１回目でＣが５点取ってリードしたのですが、そのときＤは４点取っています。

２回目が終わった時点で、Ｄが一人リードするためには、Ｄは５点取る必要があり、このため他の人の取った得点が判ります。

２回目までの途中結果を表２に示します。（表で　/　の左の数がその回に取った得点、右の数が合計点です）

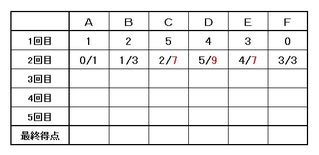
▲表２．２回目までの途中結果

このゲームでは、３、４、５回目の試行でＡが高得点を取って一人が勝つのですから、２回目の終わった時点で得点差の大きいＤやＣ、Ｅなどを逆転しなければなりません。そこで、表１を修正して、Ａと他の人との得点差を示す表３を作ります。

▲表３．Ａと他の人との得点差

これで準備完了です。まず、ＡとＤは２回目終了時点で８点差あるので、Ａは３～５回目でＤに対して９点差以上上回ることが必要です。

そのためには、表３の左にある①から⑥の試行のうち、条件に合う組み合わせを（　，　，　）で表すと、それは、
（④，④，③）（＋９）←（ＡのＤに対する得点差）
（④，④，④）（＋１５）
（④，④，⑤）（＋１３）
（④，④，⑥）（＋１１）
（④，⑤，⑥）（＋９）
（⑤，⑤，⑤）（＋９）
と６通りの場合があります。

同様にＣを逆転するためには、６点差をひっくり返す必要があるので、Ａは３～５回目でＣに対して７点差以上上回ることが必要です。これを前と同じように表すと、
（⑤，④，④）（＋８）←（ＡのＣに対する得点差）
（⑤，④，⑥）（＋８）
（⑤，⑤，④）（＋１０）
（⑤，⑤，⑤）（＋１２）
（⑤，⑤，⑥）（＋１０）
（⑤，⑥，⑥）（＋８）
と６通りの場合があります。

さらにＥを逆転するためには、６点差をひっくり返す必要があるので、Ａは３～５回目でＥに対して７点差以上上回ることが必要です。これを前と同じように表すと、
（④，④，③）（＋１０）←（ＡのＥに対する得点差）
（④，④，④）（＋１２）
（④，④，⑤）（＋１０）
（④，③，⑤）（＋８）
（④，③，③）（＋８）
（④，⑤，⑤）（＋８）
と６通りの場合があります。

以上の３つのグループの組合せのなかで共通するものが、ＡがＤ、Ｃ、Ｅに勝つ試行の組合せになり、それは（④，④，⑤）だけです。

そこで、この場合の各人の得点を調べると、表４にあるように、
Ａ：１５点、Ｂ：１４点、Ｃ：１３点、Ｄ：１０点、Ｅ：１１点、Ｆ：１２点
となり、Ａ一人が勝つことが確認できたので、これが答えになります。

▲表４．最終結果

数学・算数に限ったことではありませんが、特に数学・算数の問題では、図表を活用することが大切です。面倒臭がらず図表を書いて問題に立ち向かいましょう。