こんにちは。東久留米市の学習塾塾長です。
ここ数日の良い天気とは違って、雲が多く少し風もある日になりました。雨は降らないようですが、明日も曇りになるようです。
さて、今回は平成22年度東大大学院新領域創成科学研究科海洋技術環境学の入試問題で、
問題は、
「3次元直交座標系x、y、zにおける次の4点を頂点とする四面体の体積を求めなさい。
A(0,1,1)、B(1,1,3)、C(4,7,3)、D(3,4,-5) 」
です。
四面体の体積を求める方法は、ベクトルの外積・内積を使う方法、行列式を使う方法などがありますが、ここでは、3個の頂点で決まる平面を底面とし、残りの頂点と底面との距離を求めて、四角錐の体積を計算しましょう。
図1に、問題に与えられた4個の頂点とそれらによって作られる四角錐を示します。

▲図1.4弧の頂点と四角錐
ここで、図2に示すように、頂点Aを原点に平行移動します。すると、 B(1,0,2)、C(4,6,2)、D(3,3,-6)になります。
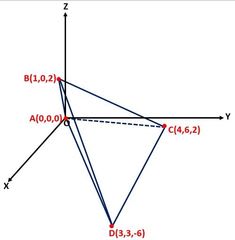
▲図2.頂点Aを原点に平行移動しました
準備ができたところで、まず、四角錐の底面を△BCDとしてその面積を求めます。底面の三角形の底辺をBCとすると、
BC=√((4-1)^2+(6-0)^2+(2-2)^2)
=3√5
です。
次に直線BCの式は、
y=2x-2
z=2
です。
そこで、直線BC上の点P(p,2p-2、2)として、頂点Dと点Pとの距離をLとすると、
L^2=(p-3)^2+(2p-2-3)^2+(2-(-6))^2
=5p^2-26p+98
=5(p-13/5)^2+321/5
となります。
これから、頂点Dから直線BCまでの距離、つまり、△BCDで辺BCを底辺としたときの高さhは、
h=√(321/5)
になります。
したがって、△BCDの面積Sは、
S=1/2・3√5・√(321/5)
=3/2・√321
です。
続いて、頂点Aと底面BCDとの距離を求めましょう。そのためには、平面BCDの式が必要なので、それを
ax+by+cz+d=0 (1)
とします。
この平面上に頂点B、C、Dがあることから、
a +2c+d=0
4a+6b+2c+d=0
3a+3b-6c+d=0
が成り立ちます。
これらから、
b=-a/2
c=a/16
d=-9a/8
となり、これらを(1)に代入し整理すると、平面BCDの式は、
16x-8y+z-18=0
となります。
次に、頂点Aと平面BCDとの距離を求めるのですが、前回のように平面上の点Q(s、t、-16s+8t+18)として、AQの距離L’をsとtで表し、平方完成を2回することで、AQの最小値を求めることができます。
この結果だけを紹介すると、
L’=s^2+t^2+(-16s+8t+18)^2
=257(s-32(4t+9)/257)^2+321/257・(t+48/107)^2+108/107
となり、これから頂点Aと平面BCDとの距離は、√(108/107)(=18/√321)です。
ここでは、前回紹介した点(x0,y0,z0)と平面ax+by+cz+d=0との距離の公式
lax0+by0+cz0+dl/√(a^2+b^2+c^2)
を使いましょう。
x0=y0=z0=0、a=16、b=-8、c=1なので、頂点Aと平面BCDとの距離L”は、
L”=l0+0+0-18l/√(256+64+1)
=18/√321
です。
以上から、四角錐ABCDの体積Vは、
V=1/3・3/2・√321・18/√321
=9
となり、これが答えです。
ついでに行列式を使う方法も紹介します。
四角錐の1つの頂点を原点にして、残りの3個の頂点の座標値を並べて行列Mを作ります。すると、四角錐の体積Vは、
V=1/6ldet(M)l
となります。ここで、ldet(M)lは、行列Mの行列式の絶対値を表します。
本問では、頂点Aを原点にすると、B(1,0,2)、C(4,6,2)、D(3,3,-6)なので、行列Mは図3のようになります。
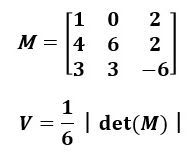
▲図3.行列式を使う方法
すると、
det(M)=1・6・(-6)+0・2・3+2・3・4-2・6・3-0・4・(-6)-1・3・2 ←(サラスの公式を使いました)
=-36+24-36-6
=-54
で、四面体の体積Vは、
V=1/6・l-54l
=9
と簡単に計算することができます。
最後の行列式を使った方法は、平面上での三角形の面積にも使えます。三角形の1つの頂点を原点に平行移動させて、残りの2個の頂点を(x1,y1)、(x2,y2)とすると、三角形の面積Sは、S=1/2・ldet(M)l=1/2・lx1y2-x2y1lになります。興味のある人は確かめてみて下さい。
ここ数日の良い天気とは違って、雲が多く少し風もある日になりました。雨は降らないようですが、明日も曇りになるようです。
さて、今回は平成22年度東大大学院新領域創成科学研究科海洋技術環境学の入試問題で、
問題は、
「3次元直交座標系x、y、zにおける次の4点を頂点とする四面体の体積を求めなさい。
A(0,1,1)、B(1,1,3)、C(4,7,3)、D(3,4,-5) 」
です。
四面体の体積を求める方法は、ベクトルの外積・内積を使う方法、行列式を使う方法などがありますが、ここでは、3個の頂点で決まる平面を底面とし、残りの頂点と底面との距離を求めて、四角錐の体積を計算しましょう。
図1に、問題に与えられた4個の頂点とそれらによって作られる四角錐を示します。

▲図1.4弧の頂点と四角錐
ここで、図2に示すように、頂点Aを原点に平行移動します。すると、 B(1,0,2)、C(4,6,2)、D(3,3,-6)になります。

▲図2.頂点Aを原点に平行移動しました
準備ができたところで、まず、四角錐の底面を△BCDとしてその面積を求めます。底面の三角形の底辺をBCとすると、
BC=√((4-1)^2+(6-0)^2+(2-2)^2)
=3√5
です。
次に直線BCの式は、
y=2x-2
z=2
です。
そこで、直線BC上の点P(p,2p-2、2)として、頂点Dと点Pとの距離をLとすると、
L^2=(p-3)^2+(2p-2-3)^2+(2-(-6))^2
=5p^2-26p+98
=5(p-13/5)^2+321/5
となります。
これから、頂点Dから直線BCまでの距離、つまり、△BCDで辺BCを底辺としたときの高さhは、
h=√(321/5)
になります。
したがって、△BCDの面積Sは、
S=1/2・3√5・√(321/5)
=3/2・√321
です。
続いて、頂点Aと底面BCDとの距離を求めましょう。そのためには、平面BCDの式が必要なので、それを
ax+by+cz+d=0 (1)
とします。
この平面上に頂点B、C、Dがあることから、
a +2c+d=0
4a+6b+2c+d=0
3a+3b-6c+d=0
が成り立ちます。
これらから、
b=-a/2
c=a/16
d=-9a/8
となり、これらを(1)に代入し整理すると、平面BCDの式は、
16x-8y+z-18=0
となります。
次に、頂点Aと平面BCDとの距離を求めるのですが、前回のように平面上の点Q(s、t、-16s+8t+18)として、AQの距離L’をsとtで表し、平方完成を2回することで、AQの最小値を求めることができます。
この結果だけを紹介すると、
L’=s^2+t^2+(-16s+8t+18)^2
=257(s-32(4t+9)/257)^2+321/257・(t+48/107)^2+108/107
となり、これから頂点Aと平面BCDとの距離は、√(108/107)(=18/√321)です。
ここでは、前回紹介した点(x0,y0,z0)と平面ax+by+cz+d=0との距離の公式
lax0+by0+cz0+dl/√(a^2+b^2+c^2)
を使いましょう。
x0=y0=z0=0、a=16、b=-8、c=1なので、頂点Aと平面BCDとの距離L”は、
L”=l0+0+0-18l/√(256+64+1)
=18/√321
です。
以上から、四角錐ABCDの体積Vは、
V=1/3・3/2・√321・18/√321
=9
となり、これが答えです。
ついでに行列式を使う方法も紹介します。
四角錐の1つの頂点を原点にして、残りの3個の頂点の座標値を並べて行列Mを作ります。すると、四角錐の体積Vは、
V=1/6ldet(M)l
となります。ここで、ldet(M)lは、行列Mの行列式の絶対値を表します。
本問では、頂点Aを原点にすると、B(1,0,2)、C(4,6,2)、D(3,3,-6)なので、行列Mは図3のようになります。
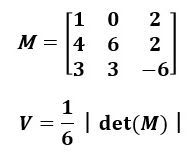
▲図3.行列式を使う方法
すると、
det(M)=1・6・(-6)+0・2・3+2・3・4-2・6・3-0・4・(-6)-1・3・2 ←(サラスの公式を使いました)
=-36+24-36-6
=-54
で、四面体の体積Vは、
V=1/6・l-54l
=9
と簡単に計算することができます。
最後の行列式を使った方法は、平面上での三角形の面積にも使えます。三角形の1つの頂点を原点に平行移動させて、残りの2個の頂点を(x1,y1)、(x2,y2)とすると、三角形の面積Sは、S=1/2・ldet(M)l=1/2・lx1y2-x2y1lになります。興味のある人は確かめてみて下さい。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます