こんにちは。東久留米市の学習塾塾長です。
小5の塾生が取り組んでいる公立中高一貫校対策問題集にある、天秤を使って10個のボールから重さの異なる1個のボールを見つけ出す問題を取り上げます。
問題は、
「ここに10個のボールがあります。見た目はまったく同じですが、1つだけ重さのちがうボールが混ざっています。この中から重さのちがうボールを見つけるために、てんびんを3回使って調べたところ、下の図のようになりました。10個の玉を①②③④⑤⑥⑦⑧⑨⑩とするとき、あとの問いに答えましょう。
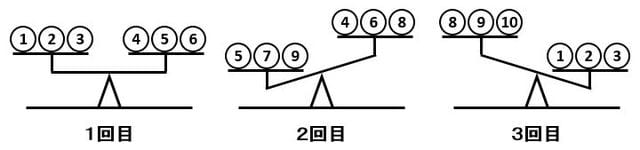
▲問題図
(1) 1回目と2回目の結果から、重さのちがうと思われるボールは何番だと考えられますか。可能性のあるものをすべて答えましょう。
(2) 3回目の結果をあわせると、重さのちがうボールは何番になりますか。また、そのボールは重いですか。軽いですか。」
です。
早速、取り掛かりましょう。
1回目の結果から、①②③④⑤⑥のボールの重さはすべて同じであることが判ります。
そこで図1のように、1回目と2回目について、これらのボールを青色でマークしましょう。

▲図1.1回目と2回目の①②③④⑤⑥のボールを青色でマークしました
すると青色でマークされていないボールは⑦⑧⑨なので、重さの違う可能性のあるボールは ⑦⑧⑨ で、これが答えです。
次に(2)です。
上の結果から、重さの異なるボールは、
[1]⑦か⑨のどちらかが重い
[2]⑧が軽い
のいずれかになります。
一方、図2のように、3番目の右側の皿にあるボールはすべて同じ重さですから、その反対側の左側の皿にある⑧⑨⑩のなかに、軽いボールが混ざっていることになります。

▲図2.3番目の左側の皿に軽いボールが混ざっています
ところが、 [1] [2] から軽いボールである可能性のあるのは⑧だけなので、重さの異なるボールは ⑧ で、それは 軽い ことになります。
n個のもの(金貨、錘、玉など)から1個の重さの異なるものを天秤を使って見つけ出すパズルは昔から有名で、あらかじめ軽重が分かっている場合、天秤をk回使用するときに見分けることのできる n は、
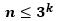
で、軽重が分かっていない場合(ただし、重さが異なる1個のものを見分けるだけで、その軽重は問いません)、

になります。興味のある人は調べてみてください。
小5の塾生が取り組んでいる公立中高一貫校対策問題集にある、天秤を使って10個のボールから重さの異なる1個のボールを見つけ出す問題を取り上げます。
問題は、
「ここに10個のボールがあります。見た目はまったく同じですが、1つだけ重さのちがうボールが混ざっています。この中から重さのちがうボールを見つけるために、てんびんを3回使って調べたところ、下の図のようになりました。10個の玉を①②③④⑤⑥⑦⑧⑨⑩とするとき、あとの問いに答えましょう。

▲問題図
(1) 1回目と2回目の結果から、重さのちがうと思われるボールは何番だと考えられますか。可能性のあるものをすべて答えましょう。
(2) 3回目の結果をあわせると、重さのちがうボールは何番になりますか。また、そのボールは重いですか。軽いですか。」
です。
早速、取り掛かりましょう。
1回目の結果から、①②③④⑤⑥のボールの重さはすべて同じであることが判ります。
そこで図1のように、1回目と2回目について、これらのボールを青色でマークしましょう。

▲図1.1回目と2回目の①②③④⑤⑥のボールを青色でマークしました
すると青色でマークされていないボールは⑦⑧⑨なので、重さの違う可能性のあるボールは ⑦⑧⑨ で、これが答えです。
次に(2)です。
上の結果から、重さの異なるボールは、
[1]⑦か⑨のどちらかが重い
[2]⑧が軽い
のいずれかになります。
一方、図2のように、3番目の右側の皿にあるボールはすべて同じ重さですから、その反対側の左側の皿にある⑧⑨⑩のなかに、軽いボールが混ざっていることになります。

▲図2.3番目の左側の皿に軽いボールが混ざっています
ところが、 [1] [2] から軽いボールである可能性のあるのは⑧だけなので、重さの異なるボールは ⑧ で、それは 軽い ことになります。
n個のもの(金貨、錘、玉など)から1個の重さの異なるものを天秤を使って見つけ出すパズルは昔から有名で、あらかじめ軽重が分かっている場合、天秤をk回使用するときに見分けることのできる n は、
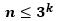
で、軽重が分かっていない場合(ただし、重さが異なる1個のものを見分けるだけで、その軽重は問いません)、

になります。興味のある人は調べてみてください。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます