こんにちは。東久留米市の学習塾塾長です。
現在の東久留米の気温は26℃で午後には28℃に達する予想です。晩には、「真田丸」を観ながら素麺を食べることにします。
さて、今回は2013年日本数学オリンピック予選に出題された整数問題を取り上げます。
問題は、
「3つの正の整数x、y、zの最小公倍数が2100であるとき、x+y+zとしてありうる最小の値を求めよ。」
です。
早速、取り掛かりましょう。
まず、2100を素因数分解すると、
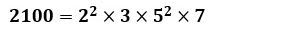
です。
したがって、x、y、zは

という形で表すことが」できます。
そこで、x、y、zを

とすると、
0≦a,e,i≦2、a、e、iのうち少なくとも1つは2
0≦b,f,j≦1、b、f、jのうち少なくとも1つは1
0≦c,g,k≦2、c、g、kのうち少なくとも1つは2
0≦d,h,l≦1、d、h、lのうち少なくとも1つは1
のとき、x、y、zの最小公倍数は2100になります。
さらに、x+y+zが取り得る最小値を求めるので、
a、e、iのうち1つが2で他は0
b、f、jのうち1つが1で他は0
c、g、kのうち1つが2で他は0
d、h、lのうち1つが1で他は0
になります。
つまり、
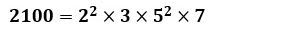
を構成する4組の数(2^2、3、5^2、7)を、どのようにx、y、zに振り分ければ、x+y+zを最小にできるかということになります。
そこで、
S(n)=x+y+z (n=1,2,3,4)
とし、このS(n)に2^2=4、3、5^2=25、7の4つの数を大きい順(25→7→4→3)に代入してS(4)を最小とするx、y、zの組合せを見つけます。
まず、初めに25を代入するのですが、x、y、zのどれに代入してもS(1)の値は同じですから、ここではxに代入し、
S(1)=25+y+z
です。
そして、繰り返しxに代入できるように、
S(2)=25x+y+z
とします。
次に、7を代入するのですが、S(2)をxの関数とみたとき、その変化の割合は25であるのに対し、S(2)をyまたはzの関数とみたとき、その変化の割合は1でです。
つまり、7をxに代入するより、yまたはzに代入するほうがS(2)を小さくすることができます。
そこで、ここでは7をyに代入し、
S(2)=25x+7+z
とします。
そして、
S(3)=25x+7y+z
とします。
続いて、4を代入するのですが、S(3)をx、yの関数とみたとき、それぞれの変化の割合は25と7であるのに対し、S(3)をzの関数とみたとき、その変化の割合は1です。
つまり、4をzに代入したとき、S(3)を小さくすることができます。
そこで、4をzに代入し、
S(3)=25x+7y+4
です。
そして、
S(4)=25x+7y+4z
とします。
最後に、3を代入しますが、S(4)をx、yの関数とみたとき、それぞれの変化の割合は25と7であるのに対し、S(4)をzの関数とみたとき、その変化の割合は4です。
つまり、3をzに代入したとき、S(4)を小さくすることができます。
そこで、3をzに代入し、
S(4)=25x+7y+12
です。
以上からx+y+zが最小になるのは、x、y、zの3つの数が、25、12、7になるときで、その最小値S’は、
S’=25+7+12
=44
です。
途中で「4つの数を大きい順(25→7→4→3)に代入して」としましたが、これを例えば25→4→3→7とすると、
S(2)=25x+4y+z
S(3)=25x+4y+3z
S(4)=25x+4y+21z
になり、x+y+z=25+4+21=50と最小値になりません。(この辺のところはさらに工夫が必要です。今晩、ビールを飲みながら考えてみます)
現在の東久留米の気温は26℃で午後には28℃に達する予想です。晩には、「真田丸」を観ながら素麺を食べることにします。
さて、今回は2013年日本数学オリンピック予選に出題された整数問題を取り上げます。
問題は、
「3つの正の整数x、y、zの最小公倍数が2100であるとき、x+y+zとしてありうる最小の値を求めよ。」
です。
早速、取り掛かりましょう。
まず、2100を素因数分解すると、
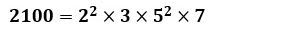
です。
したがって、x、y、zは

という形で表すことが」できます。
そこで、x、y、zを

とすると、
0≦a,e,i≦2、a、e、iのうち少なくとも1つは2
0≦b,f,j≦1、b、f、jのうち少なくとも1つは1
0≦c,g,k≦2、c、g、kのうち少なくとも1つは2
0≦d,h,l≦1、d、h、lのうち少なくとも1つは1
のとき、x、y、zの最小公倍数は2100になります。
さらに、x+y+zが取り得る最小値を求めるので、
a、e、iのうち1つが2で他は0
b、f、jのうち1つが1で他は0
c、g、kのうち1つが2で他は0
d、h、lのうち1つが1で他は0
になります。
つまり、
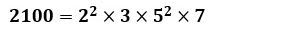
を構成する4組の数(2^2、3、5^2、7)を、どのようにx、y、zに振り分ければ、x+y+zを最小にできるかということになります。
そこで、
S(n)=x+y+z (n=1,2,3,4)
とし、このS(n)に2^2=4、3、5^2=25、7の4つの数を大きい順(25→7→4→3)に代入してS(4)を最小とするx、y、zの組合せを見つけます。
まず、初めに25を代入するのですが、x、y、zのどれに代入してもS(1)の値は同じですから、ここではxに代入し、
S(1)=25+y+z
です。
そして、繰り返しxに代入できるように、
S(2)=25x+y+z
とします。
次に、7を代入するのですが、S(2)をxの関数とみたとき、その変化の割合は25であるのに対し、S(2)をyまたはzの関数とみたとき、その変化の割合は1でです。
つまり、7をxに代入するより、yまたはzに代入するほうがS(2)を小さくすることができます。
そこで、ここでは7をyに代入し、
S(2)=25x+7+z
とします。
そして、
S(3)=25x+7y+z
とします。
続いて、4を代入するのですが、S(3)をx、yの関数とみたとき、それぞれの変化の割合は25と7であるのに対し、S(3)をzの関数とみたとき、その変化の割合は1です。
つまり、4をzに代入したとき、S(3)を小さくすることができます。
そこで、4をzに代入し、
S(3)=25x+7y+4
です。
そして、
S(4)=25x+7y+4z
とします。
最後に、3を代入しますが、S(4)をx、yの関数とみたとき、それぞれの変化の割合は25と7であるのに対し、S(4)をzの関数とみたとき、その変化の割合は4です。
つまり、3をzに代入したとき、S(4)を小さくすることができます。
そこで、3をzに代入し、
S(4)=25x+7y+12
です。
以上からx+y+zが最小になるのは、x、y、zの3つの数が、25、12、7になるときで、その最小値S’は、
S’=25+7+12
=44
です。
途中で「4つの数を大きい順(25→7→4→3)に代入して」としましたが、これを例えば25→4→3→7とすると、
S(2)=25x+4y+z
S(3)=25x+4y+3z
S(4)=25x+4y+21z
になり、x+y+z=25+4+21=50と最小値になりません。(この辺のところはさらに工夫が必要です。今晩、ビールを飲みながら考えてみます)





















※コメント投稿者のブログIDはブログ作成者のみに通知されます