中学生でも解ける東大大学院入試問題（１７０）

こんにちは。東久留米市の学習塾塾長です。

昨日より少し暖かくなりましたが、ぐずついた天気で、夜には強い雨になるようです。晴れ間が戻るのは明後日で少しの辛抱です。

さて、今回は平成１７年度東大大学院工学系研究科システム量子工学の入試問題です。

問題は、
「ビンゴゲームを考える。一枚のカードには５×５の計２５個のマス目があり、最初から開いている真ん中のマス目を抜いた２４箇所に１から９０の数字が重複することなく割り当てられている。司会者が１から９０までの数字をひとつずつ無作為に選んで読み上げていくときに、もっとも遅くビンゴが完成する（縦、横、斜めのいずれか一列の数字がすべて読み上げられる）のは、いくつ目の数字が読み上げられたときか。また、このような事象が起きる確率を求めよ。ただし階乗記号を用いて答えてよい。

」

です。

ビンゴが完成しないためには、少なくとも縦に１つずつ当たっていない（読み上げられていない）マスがなければならないので、最小５つの当たりでないマスが必要です。

さらに、これらの５つのマスを図１のように適当に配置することにより、横、斜めにも少なくとも１つの当たりでないマスを置くことができます。つまり、もっとも遅くビンゴが完成するのは、当たりでないマスが４つになるときで、それは、９０－４＝８６（番目）ということになります。

図１．当たりでない５つのマスでビンゴが完成しない例

次に、それが起きる確率を調べます。

司会者が１から９０までの数字を読み上げる場合の数は、９０×８９×・・・×１＝９０！（通り）です。

一方、当たりでない５つの数字を除いた８５個の数字を１から８５番目に読み上げる場合の数は、８５×８４×・・・×１＝８５！で、当たりでない５つの数字を８６番目から９０番目に読み上げる場合の数は、５×４×・・・×１＝５！になります。

つまり、８５番目の数字を読み上げられたとき、図１の配置ができる確率ｐは、
ｐ＝８５！５！/９０！
になります。

したがって、このｐにビンゴが完成しない５マスの配置数を乗じれば、もっとも遅くビンゴが完成する確率を求めることができます。

そこでまず、斜めにビンゴが完成しない場合を調べます。

斜めにビンゴが完成しないためには、図２に示した緑色のマスに当たりでないマスがある必要があります。

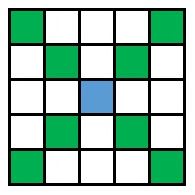
▲図２．斜めにビンゴが完成しないために当たりでないマスが置かれる位置

さらに、右上から左下、および、左上から右下の斜めに１つずつ当たりでないマスが置かれる必要があり、かつ、その２つは、同じ縦および横にあってはなりません。

つまり、斜めにビンゴが完成しないための２コマの配置は、図３の配置を、５×５のマスの中心を回転の中心として０°、９０°、１８０°、２７０°の回転移動した配置と、それらの各々について、５×５のマスの対角線（以下、対角線）を対称軸とする対称移動した配置になります。（但し、この２つの移動によってできる配置には重複するものがあるので注意が必要です）

図３．斜めにビンゴが完成しないための基本配置

そこで、図３の基本配置を元に残りの３つのコマの配置を調べると、図４のようになります。

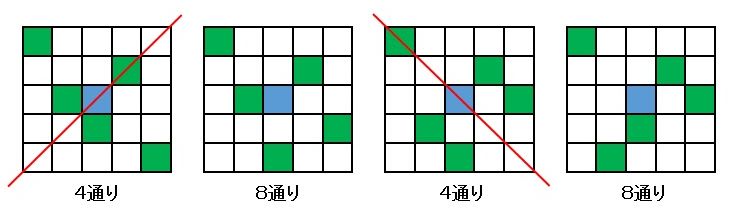
図４．ビンゴが完成しない配置

図４の左から２つ目と４つ目の配置からは、０°、９０°、１８０°、２７０°の回転移動と対角線を対称の軸とする対称移動で８通りの異なる配置を作ることができます。

ところが、左から１つ目と３つ目の配置は対角線が対称軸になっているので、０°、９０°、１８０°、２７０°の回転移動で作った４通りの異なる配置に対して、対角線を対称軸とした対称移動で同じ配置ができることになります。したがって、左から１つ目と３つ目からは、４通りの異なる配置を作ることができます。

以上により、ビンゴが完成しないすべての配置数は、８＋８＋４＋４＝２４で、２４×ｐ＝２４×８５！×５！/９０！＝２/３６６２４３９　が答えになります。


配置数の勘定方法について、もう少しスマートな方法がありそうです。少し調べてみますが、ご存知の方がいらっしゃれば教えてください。