日本数学オリンピックの簡単な問題（６０）

こんにちは。東久留米市の学習塾塾長です。

高気圧が日本を広く覆っていて、九州以外は全国的に晴れマーク一色です。東久留米も雲ひとつない秋晴れで、気温は２１°、湿度は５１％と快適な日になりました。明日もいい天気になるようです。

さて、今回は２０００年日本数学オリンピック予選に出題された図形問題を取り上げます。

問題は、
「数のように直角三角形内に３つの正方形と３つの円Ｏ1、Ｏ2、Ｏ3があり、各円はそれぞれを含む小直角三角形の内接円であり、Ｏ1、Ｏ3の直径の長さはそれぞれ９、４である。円Ｏ2の直径の長さを求めよ。
　なお、この図は１８５３年に佐々木萬蔵が陸奥の国（現在の岩手県）三陸綾里八幡神社に奉納した算額から取ったものである。」
です。

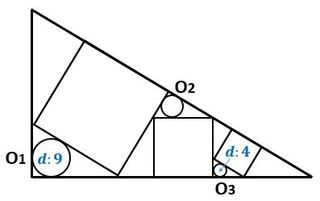
▲問題図

早速、取り掛かりましょう。

問題図の各点を、図１のように、ＡからＧとします。

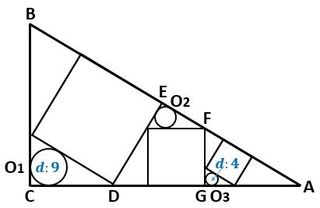
▲図１．各点をＡからＧとしました

このとき、図２に示すように、△ＡＢＣと円Ｏ1、△ＡＤＥと円Ｏ2、△ＡＦＧと円Ｏ3を含む図形は相似で、それらの相似比の関係は、
（△ＡＢＣと円Ｏ1を含む図形）：（△ＡＤＥと円Ｏ2を含む図形）＝（△ＡＤＥと円Ｏ2を含む図形）：（△ＡＦＧと円Ｏ3を含む図形）　（★）
になります。

▲図２．△ＡＢＣと円Ｏ1、△ＡＤＥと円Ｏ2、△ＡＦＧと円Ｏ3を含む図形は相似です

そこで、円Ｏ2の直径をｘとすると、（★）から
９：ｘ＝ｘ：４
ｘ^2＝３６
ｘ＝６
です。

したがって、円Ｏ2の直径は６で、これが答えです。


相似を移用すれば簡単な問題です。