こんにちは。東久留米市の学習塾塾長です。
今回は、令和2年度筑波大附属駒場中の問題です。
問題は、
「図1のように、長方形ABCDにおいて、辺ABの長さが2m、辺ADの長さが1mです。この長方形の内部に点Pを、4つの三角形PAB、PBC、PCD、PDAの面積がすべて異なるようにとります。4つの三角形を、面積の小さい順に㋐、㋑、㋒、㋓としたところ、三角形PABが㋐となり、㋐と㋑、㋑と㋒、㋒と㋓の面積の差がすべて等しくなりました。次の問いに答えなさい。
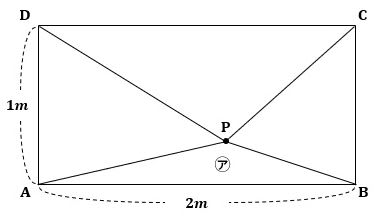
▲図1
(1) ㋐の面積が
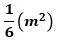
のとき、㋓の面積を求めなさい。
(2) 点Pが図2の位置にあるとき、三角形PDAが㋑です。また図2で、点Qは辺AD上、点Rは直線PQ上にあり、PQとADは垂直です。さらに、斜線で示した図形DRAPの面積は、㋐と㋑の面積の差に等しく、
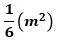
です。このとき、QRの長さを求めなさい。
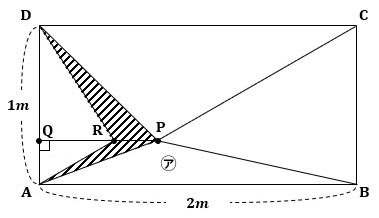
▲図2
(3) 点Pとして考えられるすべての位置を解答欄の長方形ABCDの内部にかきなさい。ただし、㋐、㋑、㋒、㋓の面積はすべて異なるので、図3の点線部分は答えに含まれません。」
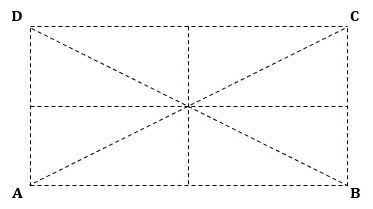
▲図3
です。
㋐と㋑、㋑と㋒、㋒と㋓の面積差をDとすると、
㋑=㋐+D
㋒=㋑+D=㋐+D×2
㋓=㋒+D=㋑+D×2=㋐+D×3
です。(㋐、㋑、㋒、㋓でそれぞれの面積を表します)
一方、
㋐+㋑+㋒+㋓=(長方形ABCDの面積)=2(m2)
が成り立ち、これに㋑、㋒、㋓を代入すると、
㋐+㋐+D+㋐+D×2+㋐+D×3=㋐×4+D×6=2(m2)
です。
このとき、
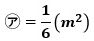
なので、
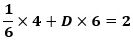
から
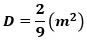
になり、したがって、
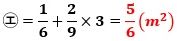
で、これが(1)の答えです。
次に(2)です。
㋐と㋑の面積差が
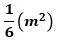
なので、
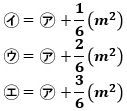
です
すると、
㋐+㋑+㋒+㋓=㋐×4+1=2(m2)
で、これから
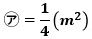
です。
このとき、三角形RDAの面積と㋐は等しいので、

で、これから、
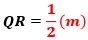
で、これが答えです。
最後の(3)です。
図4のように、長方形ABCDの対角線の交点をOとして長方形OXPYをつくり、辺OX、OYの長さをそれぞれhとdとします。
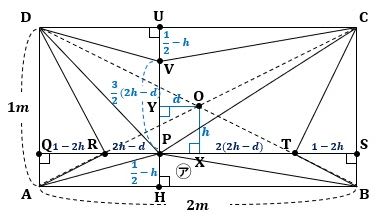
▲図4.長方形OXPYをつくりOX=h、OY=dとしました
初めに、三角形PDAが㋑になる場合(d>0)を調べます。
三角形PABの高さは、

で、この面積は三角形RDA、三角形PBC、三角形PCDの面積に等しいので、
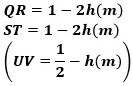
になります。(掛け算の記号×を省略しました。例えば、2hは2×hを表します)
また、
PR=QX-QR-PX
で、QX=1、QR=1-2h、PX=dから
PR=1-(1-2h)-d=2h-d(m)
です。
このとき、図形PBTCと図形PCVDの面積は、それぞれ図形PDRAの面積の2倍と3倍なので、
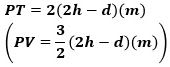
になります。
すると、
QS=QR+PR+PT+ST
=(1-2h)+(2h-d)+2(2h-d)+(1-2h)
=2h-3d+2
=2
になり、これから
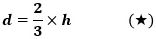
が成り立ちます。(線分HUについても(★)が導かれます)
つまり、点Pは OX:XP=3:2 になる三角形OXPの頂点になり、このとき、

なので、
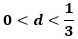
になることから、点Pとして考えられる位置は、点Oと、辺AB上で点Aから
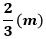
の点を結んだ線分(両端を除く)になります。
一方、三角形PBCが㋑になる場合も同様に、点Pとして考えられる位置は、点Oと、辺AB上で点Bから
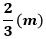
の点を結んだ線分(両端を除く)になります。
以上から、点Pとして考えられるすべての位置は、

の赤色でマークした線分(両端を除く)で、これが答えです。
簡単な問題です。
今回は、令和2年度筑波大附属駒場中の問題です。
問題は、
「図1のように、長方形ABCDにおいて、辺ABの長さが2m、辺ADの長さが1mです。この長方形の内部に点Pを、4つの三角形PAB、PBC、PCD、PDAの面積がすべて異なるようにとります。4つの三角形を、面積の小さい順に㋐、㋑、㋒、㋓としたところ、三角形PABが㋐となり、㋐と㋑、㋑と㋒、㋒と㋓の面積の差がすべて等しくなりました。次の問いに答えなさい。

▲図1
(1) ㋐の面積が
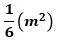
のとき、㋓の面積を求めなさい。
(2) 点Pが図2の位置にあるとき、三角形PDAが㋑です。また図2で、点Qは辺AD上、点Rは直線PQ上にあり、PQとADは垂直です。さらに、斜線で示した図形DRAPの面積は、㋐と㋑の面積の差に等しく、
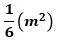
です。このとき、QRの長さを求めなさい。

▲図2
(3) 点Pとして考えられるすべての位置を解答欄の長方形ABCDの内部にかきなさい。ただし、㋐、㋑、㋒、㋓の面積はすべて異なるので、図3の点線部分は答えに含まれません。」

▲図3
です。
㋐と㋑、㋑と㋒、㋒と㋓の面積差をDとすると、
㋑=㋐+D
㋒=㋑+D=㋐+D×2
㋓=㋒+D=㋑+D×2=㋐+D×3
です。(㋐、㋑、㋒、㋓でそれぞれの面積を表します)
一方、
㋐+㋑+㋒+㋓=(長方形ABCDの面積)=2(m2)
が成り立ち、これに㋑、㋒、㋓を代入すると、
㋐+㋐+D+㋐+D×2+㋐+D×3=㋐×4+D×6=2(m2)
です。
このとき、
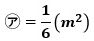
なので、
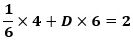
から
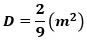
になり、したがって、
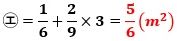
で、これが(1)の答えです。
次に(2)です。
㋐と㋑の面積差が
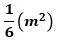
なので、
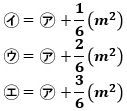
です
すると、
㋐+㋑+㋒+㋓=㋐×4+1=2(m2)
で、これから
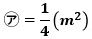
です。
このとき、三角形RDAの面積と㋐は等しいので、

で、これから、
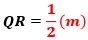
で、これが答えです。
最後の(3)です。
図4のように、長方形ABCDの対角線の交点をOとして長方形OXPYをつくり、辺OX、OYの長さをそれぞれhとdとします。

▲図4.長方形OXPYをつくりOX=h、OY=dとしました
初めに、三角形PDAが㋑になる場合(d>0)を調べます。
三角形PABの高さは、

で、この面積は三角形RDA、三角形PBC、三角形PCDの面積に等しいので、
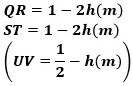
になります。(掛け算の記号×を省略しました。例えば、2hは2×hを表します)
また、
PR=QX-QR-PX
で、QX=1、QR=1-2h、PX=dから
PR=1-(1-2h)-d=2h-d(m)
です。
このとき、図形PBTCと図形PCVDの面積は、それぞれ図形PDRAの面積の2倍と3倍なので、
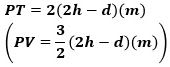
になります。
すると、
QS=QR+PR+PT+ST
=(1-2h)+(2h-d)+2(2h-d)+(1-2h)
=2h-3d+2
=2
になり、これから
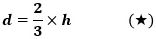
が成り立ちます。(線分HUについても(★)が導かれます)
つまり、点Pは OX:XP=3:2 になる三角形OXPの頂点になり、このとき、

なので、
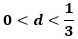
になることから、点Pとして考えられる位置は、点Oと、辺AB上で点Aから
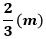
の点を結んだ線分(両端を除く)になります。
一方、三角形PBCが㋑になる場合も同様に、点Pとして考えられる位置は、点Oと、辺AB上で点Bから
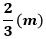
の点を結んだ線分(両端を除く)になります。
以上から、点Pとして考えられるすべての位置は、

の赤色でマークした線分(両端を除く)で、これが答えです。
簡単な問題です。





















※コメント投稿者のブログIDはブログ作成者のみに通知されます